Предмет: Алгебра,
автор: sanyaberz
Решить систему уравнений методом сложения. Кто может помочь по делу, помогите пожалуйста. Не из решатора.
Приложения:
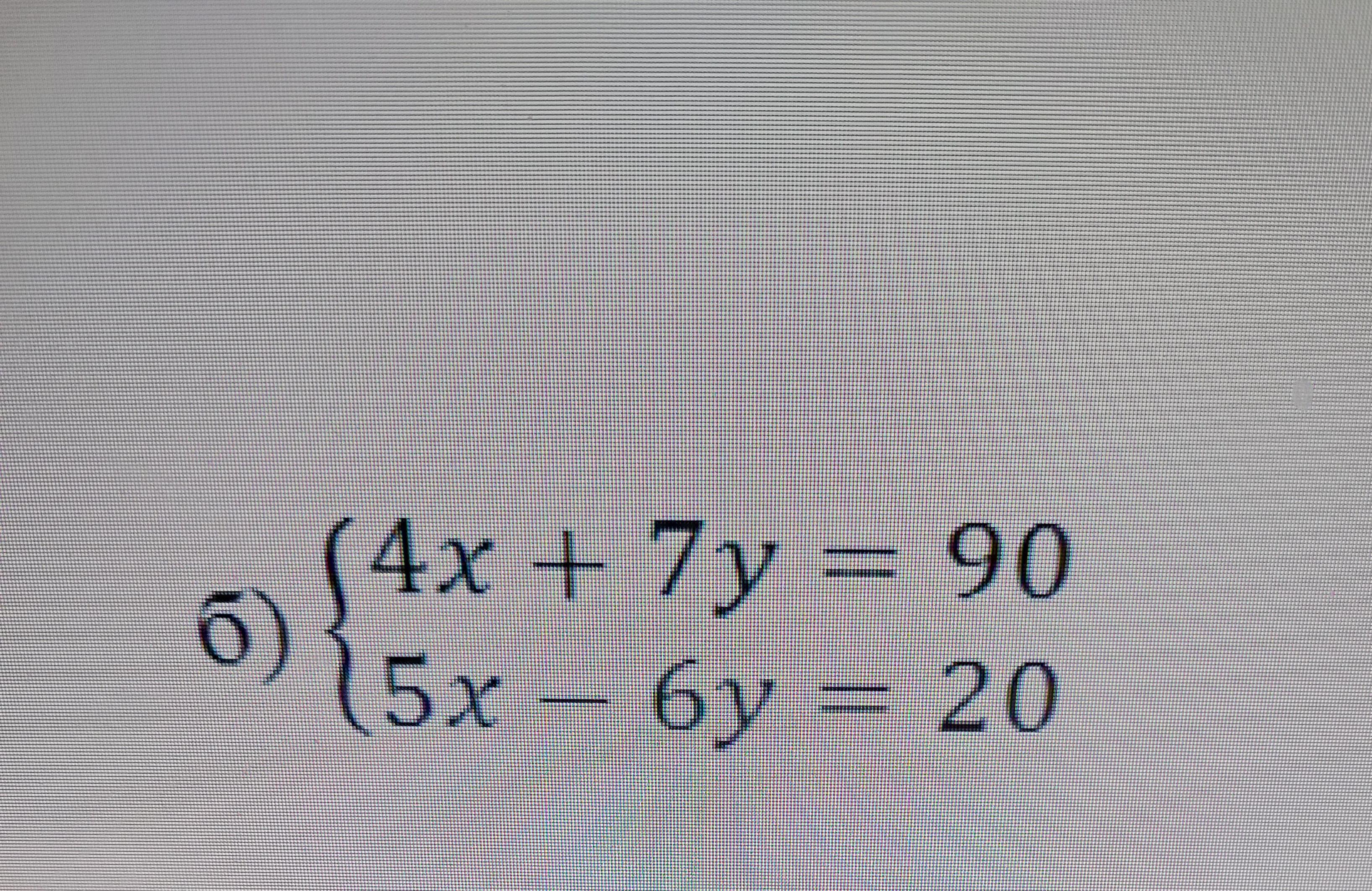
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Решить систему уравнений методом сложения :
Первое уравнение системы домножим на 5 , а второе на 4 , а затем отнимем от первого уравнения системы второе .
Из второго уравнения системы выразим x через y
Подставим
Похожие вопросы
Предмет: Русский язык,
автор: щщечзнч
Предмет: Русский язык,
автор: 27chehova
Предмет: Русский язык,
автор: л9е9р9а
Предмет: Русский язык,
автор: nikisho