Предмет: Математика,
автор: muxabig200333
Дано F(x)=cos²(x+9) найдите f,g,h так чтобы F=f•g•h
Решение : F(x)=f•g•h(x)=f(g(h(x)))=cos²(x+9)
h(x)=x+9
g(x)=cosx
f(x)=x²
Найти другой способ решения ???
НУЖНО НАЙТИ ДРУГОЙ СПОСОБ РЕШЕНИЯ
Нужно найти f , g , h другим способом, не таким которым уже сделано
Приложения:
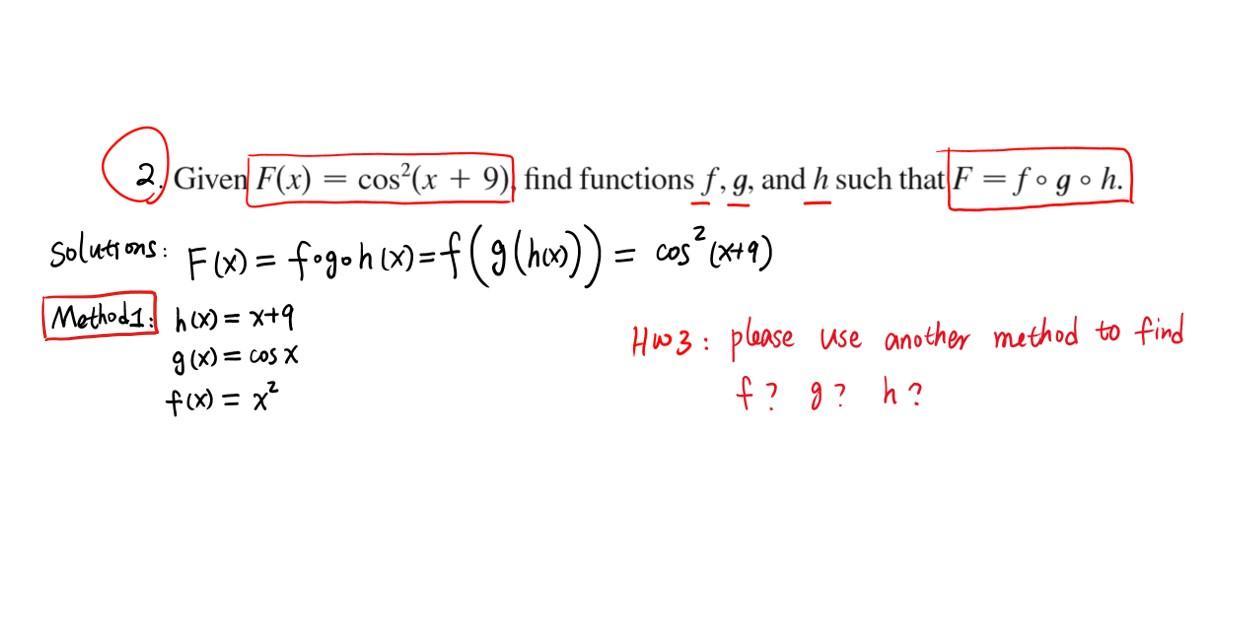
Alnadya:
а что надо сделать ?
записана сложная функция и что с ней надо сделать ? что решать : может производную взять?
Ответы
Автор ответа:
2
Ответ:
Задана сложная функция F(x) , .
Внутренняя функция линейная .
Для h(x) внешней функцией является тригонометрическая функция
косинус . ( Аргумент косинуса должен быть записан (х+9) , а не х ).
Для функции сos(х+9) внешней функцией является степенная
функция .
То есть для внешней степенной функции аргументом является тригонометрическая функция, для которой аргументом является линейная функция .
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Граня1
Предмет: Английский язык,
автор: софа306
Предмет: Українська мова,
автор: Ана1111111111111
Предмет: Математика,
автор: rubkatupka05
Предмет: Английский язык,
автор: katikati66