Помогите пожалуйста, я ничего не поняла…(
Ответы
Ответ:
Просто смотрим, какими прямыми огорожен каждый кусочек, и описываем это с помощью неравенств. Для проверки можно подставлять какие-нибудь рандомные точки. Например, удобно подставлять (0, 0), если он не попадает на прямую. Кстати, здесь я использую нестрогие неравенства, потому что прямая не пунктиром, то есть тоже входит в искомую область.
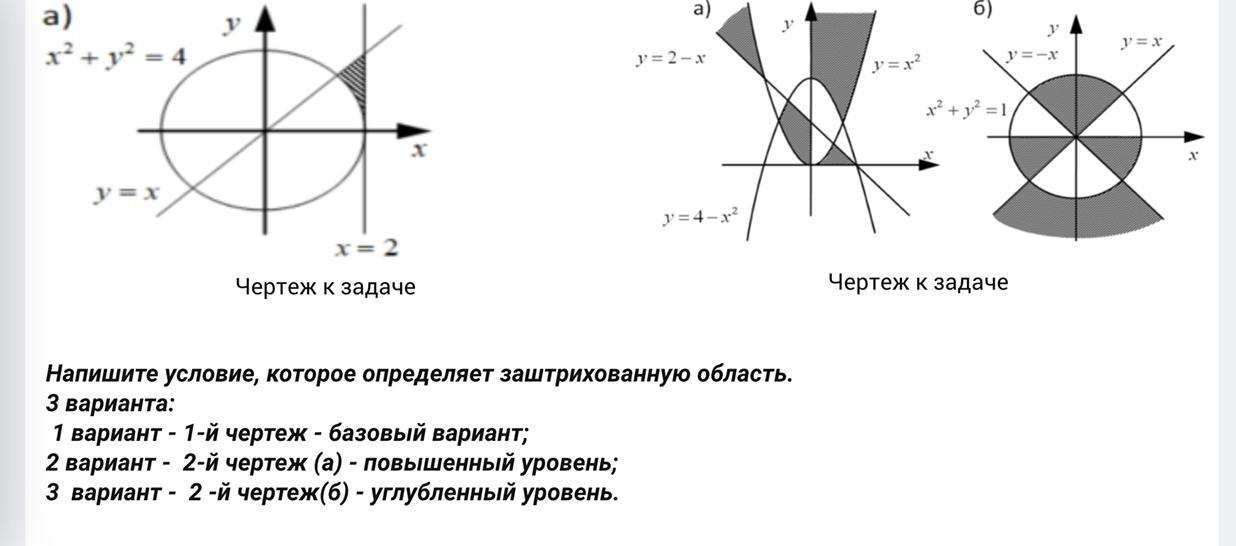
1а) (х <= 2) И (y <= x) И (x^2 + y^2 >= 4)
Объяснение:
- х <= 2 отвечает за то, что этот кусочек левее прямой х = 2
- y <= x отвечает за то, что этот кусочек ниже прямой у = х
- x^2 + y^2 >= 4 отвечает за то, что этот кусочек вне круга, то есть расстояние между ним и центром больше его радиуса (можно еще так записать поэтому: sqrt(x^2 + y^2) >= 2).
- Это все один кусочек ставим между этими условиями логическое И.
2а) (y <= x^2) И (y >= 2 - x)
ИЛИ
(y <= 2 - x) И (y <= 4 - x^2) И (x <= 0) И (y >= x^2)
ИЛИ
(y <= 2 - x) И (y >= 0) И (y <= x^2)
ИЛИ
(y >= 4 - x^2) И (x >= 0) И (y >= 0)
Объяснение:
- 1ый кусочек (самый левый):
- y <= x^2 отвечает за то, что кусочек вне параболы у = х^2
- y >= 2 - x отвечает за то, что кусочек выше прямой у = 2 - х
- 2ой кусочек (слева снизу):
- y <= 2 - x - он ниже у = х - 2
- y <= 4 - x^2 - он ниже параболы у = 4 - х^2
- x <= 0 - он меньше 0
- y >= x^2 - выше параболы y = x^2
- 3ий кусочек (снизу справа):
- y <= 2 - x - ниже прямой у = х - 2
- y >= 0 - выше оси х
- y <= x^2 - не попадает внутрь параболы y = x^2
- 4ый кусочек (справа сверху):
- y >= 4 - x^2 - выше у = 4 - х^2
- x >= 0 - правее оси у
- y >= 0 - выше оси х
В рамках одного кусочка используем для связки логическое И, но для связки условий нескольких кусочков используем логическое ИЛИ (точка же не может лежать в двух кусочках одновременно, значит лежит или в том, или в другом).
2б) (x^2 + y^2 >= 1) И (y <= x) И (y <= -x)
ИЛИ
(x^2 + y^2 <= 1) И (y <= 0) И (y >= x)
ИЛИ
(x^2 + y^2 <= 1) И (y <= 0) И (y >= -x)
ИЛИ
(x^2 + y^2 <= 1) И (y >= -x) И (y >= x)
Объяснение:
- 1ый кусочек (самый нижний):
- x^2 + y^2 >= 1 - вне окружности
- y <= x - ниже у = х
- y <= -x - ниже у = -х
- 2ой кусочек (слева):
- x^2 + y^2 <= 1 - внутри окружности
- y <= 0 - ниже оси х
- y >= x - выше у = х
- 3ий кусочек (справа):
- x^2 + y^2 <= 1 - внутри окружности
- y <= 0 - ниже оси х
- y >= -x - выше у = -х
- 4ый кусочек (верхний):
- x^2 + y^2 <= 1 - внутри окружности
- y >= -x - выше у = -х
- y >= x - выше у = х
В 1а) надо добавить " И (y >= 0)"
В 2а) надо добавить:
в 1-ую строку " И (x <= 0)"
в 5-ую строку " И (x >= 0)"
в 7-ой строке, вместо "(y >= 0)" поставить "(y >= x^2)"
Напишу условия для этих областей в виде логических выражений в Паскаль (если что, каждое проверил в своей программе, и графически оно даёт то, что нужно). Из за Паскаля, тут нет значка возведения в квадрат, это заменено просто умножением).
1а)
(x*x+y*y>=4) and (x<=2) and (y<=x) and (y>=0)
2а)
(y>=x*x) and ((y>=4-x*x) and (x>=0) or (y<=4-x*x) and (x<=0) and (y<=2-x)) or (y<=x*x) and ((y>=2-x) and (x<=0) or (y<=2-x) and (y>=0) and (x>=0))
2б)
(x*x+y*y<=1) and ((y>=x) and (y>=-x) or (y<=0) and ((y>=x) or (y>=-x))) or (x*x+y*y>=1) and (y<=x) and (y<=-x)