Question

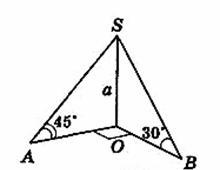
Найти расстояние между SO и АВ. Данные на рисунке

Answer 1

Найти расстояние между скрещивающимися прямыми SO и АВ.

Объяснение:

Расстояние между SO и АВ будет длина перпедикуляра из точки О на АВ . Пусть ОН⊥АВ.

Для нахождения  ОН найдем длины отрезков ЩА и ОВ из прямоугольных ΔSOA,SOB : $OA=\frac{a}{tg 45} , OB=\frac{a}{tg 30} ,$  или

$OA=\frac{a}{1} , OB=\frac{a}{\frac{1}{\sqrt{3} } } .$     ОА=а, ОВ=а√3.

ΔОАВ- прямоугольный ,  $tgOAB=\frac{OB}{OA} =\frac{a\sqrt{3} }{a} =\sqrt{3}$ ⇒ ∠OAB=60°.

ΔОАH- прямоугольный , $sinOAB=\frac{OH}{OA} , \frac{\sqrt{3} }{2} =\frac{OH}{a}$,

$OH=\frac{a\sqrt{3} }{2}$.