Question

Дан куб ABCDA1B1C1D1
Найти вектор x, удовлетворяющий равенству:
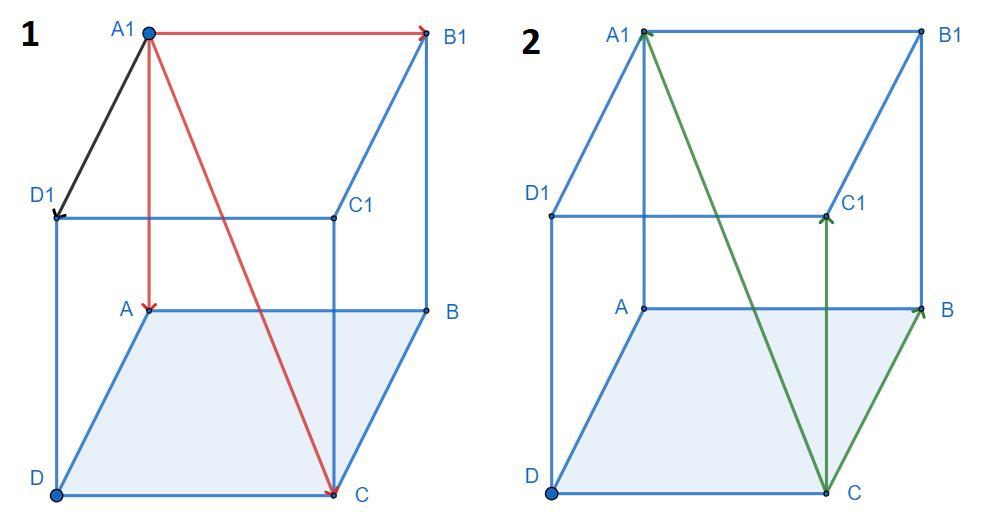
1) А1В1 + А1А + x = А1С
2) СВ + x = СА1 - СС1

Answer 1

Ответ:

1) $\overrightarrow{x} =\overrightarrow{A_1D_1}$

2) $\overrightarrow{x} =\overrightarrow{CD}$

Объяснение:

Найти вектор x, удовлетворяющий равенству:

1) $\overrightarrow{ A_1B_1} + \overrightarrow{A_1A} + \overrightarrow{x} = \overrightarrow{A_1C}$      2) $\overrightarrow{ CB} + \overrightarrow{x} = \overrightarrow{CA_1} - \overrightarrow{CC_1}$

1)  Из данного уравнения выражаем x

$\overrightarrow{x} = \overrightarrow{A_1C}-\overrightarrow{ A_1B_1} -\overrightarrow{A_1A}$

Вектора равны, если они сонаправлены и равны их длины. Отметим, что $\overrightarrow{A_1B_1} = \overrightarrow{DC}=-\overrightarrow{CD}$   и  $\overrightarrow{A_1A}=\overrightarrow{D_1D}=-\overrightarrow{DD_1}$. Значит

$\overrightarrow{x} = \overrightarrow{A_1C}-\overrightarrow{ A_1B_1} -\overrightarrow{A_1A}=\overrightarrow{A_1C}+\overrightarrow{ CD} +\overrightarrow{DD_1}=\overrightarrow{A_1D_1}$

2) Из данного уравнения выражаем x

$\overrightarrow{x} = \overrightarrow{CA_1} - \overrightarrow{CC_1}-\overrightarrow{ CB}$

Аналогично предыдущему пункту необходимо найти для вектора $-\overrightarrow{CC_1}$ найти равный ему вектор, выходящий из A₁  - это вектор $\overrightarrow{A_1A}$ - приходим в точку A - значит теперь нужно найти вектор, равный $-\overrightarrow{CB}$ и выходящий из точки A - это вектор $-\overrightarrow{DA}=\overrightarrow{AD}$. Значит

$\overrightarrow{x} = \overrightarrow{CA_1} + \overrightarrow{A_1A}+\overrightarrow{AD}=\overrightarrow{CD}$