Предмет: Математика,
автор: bighugemister
Вычислить предел с помощью правила Лопиталя: 
Ответы
Автор ответа:
1
Неопределенность 0/0, поэтому по правилу Лопиталя у знаменателя и числителя берём производные
Приложения:
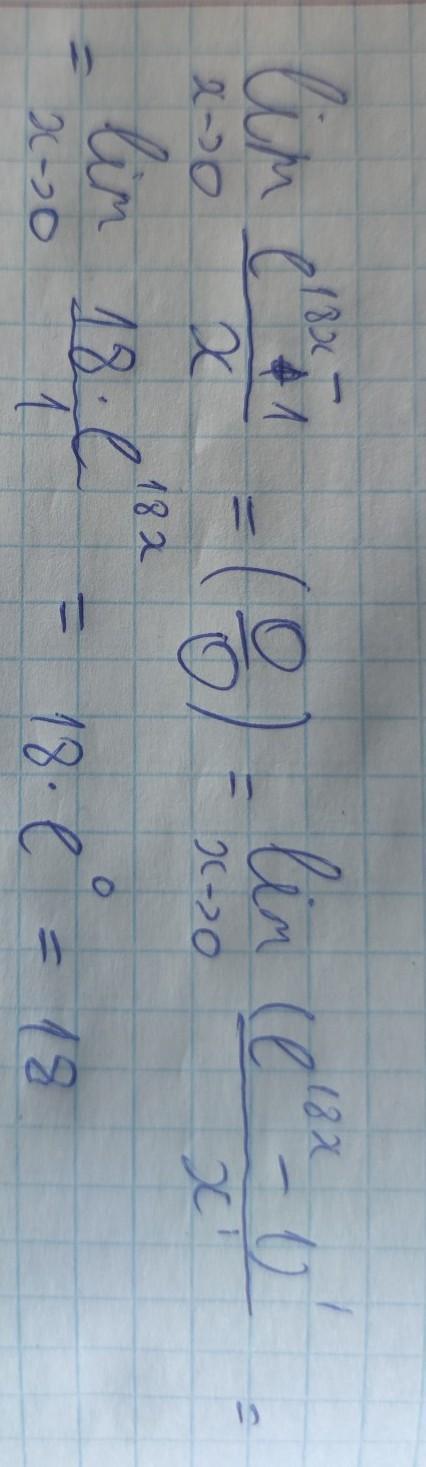
Автор ответа:
1
Ответ:
Правило Лопиталя. Неопределённость типа 0/0 .
Похожие вопросы
Предмет: Английский язык,
автор: АняПьянкова
Предмет: Окружающий мир,
автор: Valeron5112
Предмет: Окружающий мир,
автор: Detkikonfetki
Предмет: Физика,
автор: Dobriyboy
Предмет: Математика,
автор: hanzaadakazybekovaa