Question

Срочно, пожалуйста! Геометрия
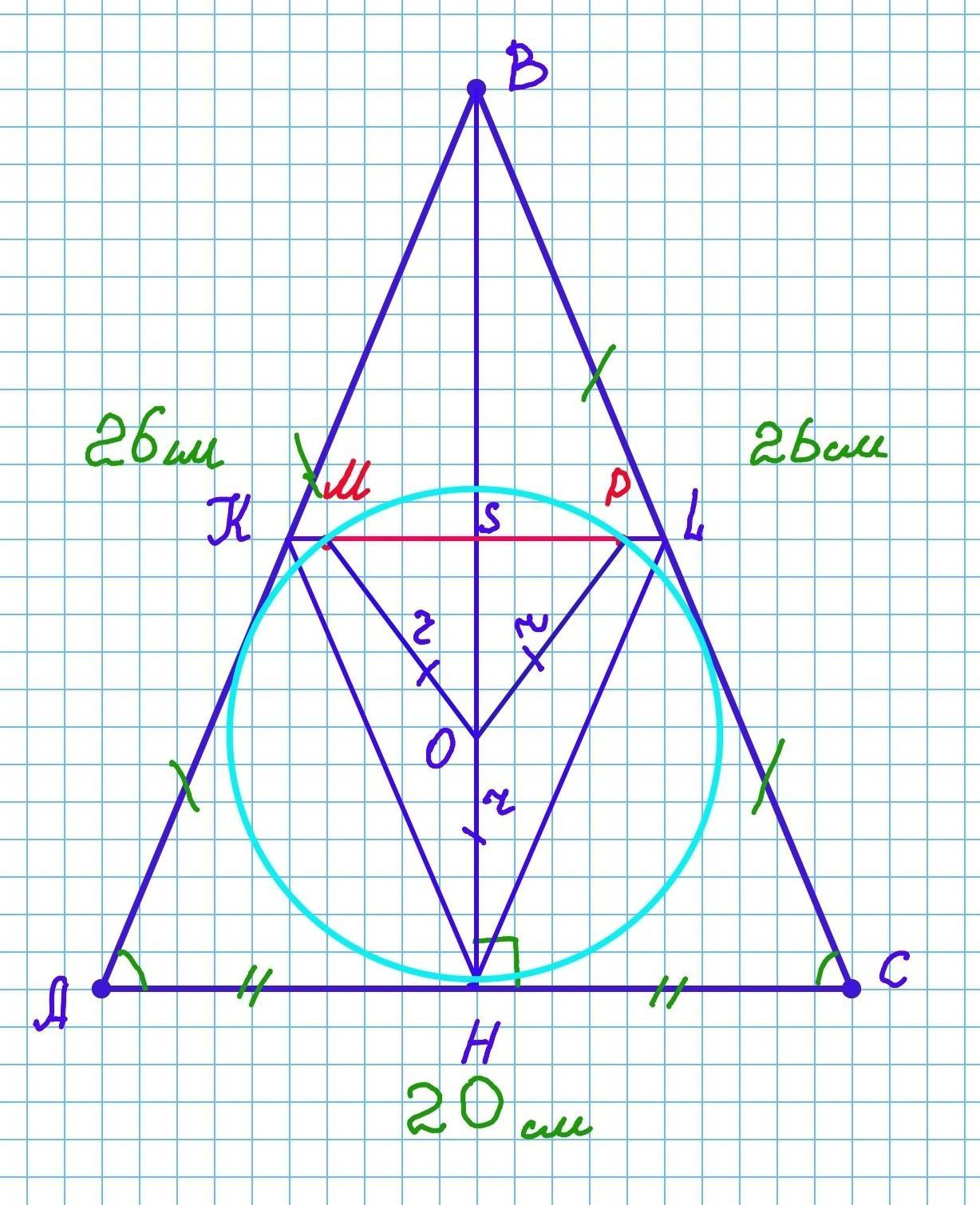
Дан треугольник ABC, в котором AB=BC=26, AC=20. Точки K и L - середины сторон AB и BC соответственно. Найдите длину той части отрезка KL, которая находится внутри вписанной в треугольник ABC окружности.

Answer 1

Дан треугольник ABC, в котором AB=BC=26, AC=20. Точки K и L - середины сторон AB и BC соответственно. Найдите длину той части отрезка KL, которая находится внутри вписанной в треугольник ABC окружности.

Ответ:

Часть отрезка, которая находится внутри вписанной в треугольник АВС окружности равна 8 см.

Пошаговое объяснение:

△АВС - равнобедренный, т,к. АВ=ВС по условию. Равные стороны называются боковыми, а нерaвная им сторона - основанием.

По свойству равнобедренного треугольника:

• углы при основании равны: ∠А=∠С
• высота BD является также биссектрисой и медианой: АН=НС=10см

KL - средняя линия треугольника АВС, т.к. точки K и L - середины сторон AB и BC ( BL=LC=13см, BK=KA=13см).

Средняя линия треугольника параллельна основанию и равна его половине:

KL=½•AC=½•20=10см.

1) Найдём радиус вписанной в треугольник АВС окружности.

r=S/p,

где р - полупериметр. р = (АВ+ВС+АС):2=(26+26+20):2=36 см

Площадь треугольника равна половине произведения его высоты на основание:

S=½•AC•BH

BH найдём из прямоугольного треугольника ВНС(∠Н=90°) по теореме Пифагора:

ВН²=ВС²-НС²=26²-10²=576. ВН=24см

Тогда площадь будет равна:

S=½•20•24=240 см²

Радиус вписанной окружности: r = 240/36=20/3 см

2) Рассмотрим треугольник HLC.

По теореме косинусов найдём сторону HL.

Для этого сначала найдём косинус угла С из прямоугольного треугольника ВНС.

Косинус угла - это отношение прилежащего катета к гипотенузе.

$cos \angle C= \dfrac{HC}{BC} = \dfrac{10}{26} = \dfrac{5}{13}$

Теперь находим НL.

НL²=LC²+HC²-2•LC•HC•cos ∠C=13²+10²-2•13•10• 5/13=169+100-100=169

НL=13см.

3)Рассмотрим △HSL. Найдём сторону HS.

Так как KL II AC, а BH⟂АС, то BH⟂KL. △HSL - прямоугольный.

Катет HS найдём по теореме Пифагора:

HS²= HL²- SL²= 13²-5²=169-25=144

HS=12см

4) Найдём длину отрезка OS.

OS=HS-OH= HS-r=12-20/3=16/3 см

5)Найдём длину отрезка SP.

Рассмотрим △OSP.

По теореме Пифагора катет SL будет равен:

$SP= \sqrt{ {OP}^{2} - {OS}^{2} } = \sqrt{ {r}^{2} - {OS}^{2} } = \\ \\ = \sqrt{ { (\frac{20}{3} })^{2} - ( { \frac{16}{3} })^{2} } = \sqrt{ \frac{400 - 256}{9} } = \\ \\ = \sqrt{ \frac{144}{9} } = \frac{12}{3} = 4$

SP=4см

6) Найдём длину отрезка MP.

MP=2•SP=2•4=8см.

Answer 2

Ответ:

Длина той части отрезка KL, которая находится внутри вписанной в треугольник ABC окружности равна 8 ед.

Пошаговое объяснение:

Требуется найти  длину той части отрезка KL, которая находится внутри вписанной в треугольник ABC окружности.

Дано: ΔАВС - равнобедренный;

AB = BC = 26, AC = 20;

Окр.О - вписана в ΔАВС;

K и L - середины сторон AB и BC;

Окр.О ∩ KL = E, P.

Найти: ЕР.

Решение:

1. Рассмотрим ΔАВС - равнобедренный.

K и L - середины сторон AB и BC.

⇒ KL - средняя линия ΔАВС.

• Средняя линия равна половине длины стороны, которую она не пересекает, и параллельна ей.

⇒ KL || АС.

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ ВН - биссектриса.

• В равнобедренном треугольнике биссектриса, проведенная к основанию, является высотой, медианой.

⇒ ВН ⊥ АС; АН = АС.

• Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к другой прямой.

⇒ ВН ⊥ KL.

2. Найдем радиус вписанной окружности.

$\displaystyle \boxed {r=\frac{S}{p};\;\;\;S=\sqrt{p(p-a)(p-b)(p-c)}; \;\;\;p=\frac{1}{2}(a+b+c) }$ ,

где a, b, c - стороны треугольника.

$\displaystyle p = (26 + 26 + 20) : 2 = 36\\\\S = \sqrt{36(36-26)(36-26)(36-20)}=240 \\\\r=\frac{240}{36}=\frac{20}{3}$

3. Рассмотрим ΔНВС - прямоугольный.

По теореме Пифагора найдем ВН.

ВС = 26; НС = АС : 2 = 10 (ВН - медиана)

ВН² = ВС² - НС² = 676 - 100 = 576;

ВН = √576 = 24.

ML || AH; BL = LC

• Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ML - средняя линия; ВМ = МН = 12.

4. Рассмотрим ΔОМР - прямоугольный.

$\displaystyle OP = \frac{20}{3};\\ \\OM=MH-OH=12-\frac{20}{3}=\frac{16}{3} \\\\MP^2=OP^2-OM^2=\frac{400}{9}-\frac{256}{9}=\frac{144}{9}=16\\ \\ MP=\sqrt{16}=4$

• Если радиус перпендикулярен хорде, то он делит ее пополам.

⇒ ЕМ = МР = 4

ЕР = ЕМ + МР = 8 (ед.)

Длина той части отрезка KL, которая находится внутри вписанной в треугольник ABC окружности равна 8 ед.