Предмет: Математика,
автор: nicatbrawl2006
здравствуйте,помогите,с разъяснениями пожалуйста
Приложения:
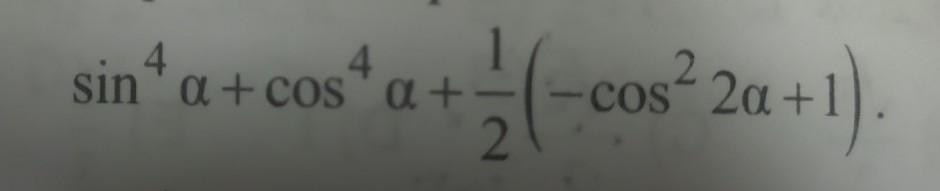
Ответы
Автор ответа:
1
Ответ:
1
Пошаговое объяснение:
1)Для начала нужно упростить выражение,используя формулу:
1-cos(a)^2=sin(a)^2
Таким образом получается такое выражение
sin(a)^4+cos(a)^4+1/2*sin(2a)^2
2)Следующий шаг.
Используя формулу sin(2a)=2sin(a)cos(a),перепишем выражение:
sin(a)^4+cos(a)^4+1/2*(2sin(a)cos(a))^2
3)Возведем эту часть выражения в степень (2sin(a)cos(a))^2=>4sin(a)^2cos(a)^2
4)Вычислим произведение:
sin(a)^4+cos(a)^4+1/2*4sin(a)^2cos(a)^2 => sin(a)^4+cos(a)^4+(4sin(a)^2cos(a)^2)/2
5)Дальше все просто.Используем формулу сокращенного умножения,а именно a^2+2ab+b^2=(a+b)^2
Таким образом,получается (sin(a)^2+cos(a)^2)^2
6)Упрощаем выражение по формуле sin(a)^2+cos(a)^2=1:
(sin(a)^2+cos(a)^2)^2 => 1^2 = 1
Ответ:1
nicatbrawl2006:
огромное спасибо
Похожие вопросы
Предмет: Русский язык,
автор: екатерина241
Предмет: Русский язык,
автор: alinaten3012
Предмет: Русский язык,
автор: xechik11
Предмет: Физика,
автор: cjucusca
Предмет: Английский язык,
автор: dureyw