Предмет: Математика,
автор: nastyasheller
Найти полный дифференциал
Приложения:
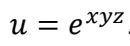
Ответы
Автор ответа:
1
Ответ:
Примечание:
Для того, чтобы найти полный дифференциал нужно сначала его записать формальном в общем виде. И затем найти частные производные. При нахождении частных производных счиатем, что диффеернцируется только, та часть по которой находится производная, а остальные части функции принимаем за константы.
По таблице производных:
Пошаговое объяснение:
Полный дифференциал функции в общем виде:
Частные производные:
Полный дифференциал функции :
Похожие вопросы
Предмет: Русский язык,
автор: биллсайфер3
Предмет: Русский язык,
автор: райзик
Предмет: Українська мова,
автор: София111145
Предмет: Алгебра,
автор: Anamiani
Предмет: География,
автор: yana4470