Question

НУЖНО СЕЙЧАС ПЖ 30 балловв треугольной пирамиде боковые ребра равны и взаимно перпендикулярны. Вычисли площадь боковой поверхности и площадь полной поверхности пирамиды если боковое ребро равно 2 дм

Answer 1

Ответ:

S(бок) = 6 кв.дм.; S(полн) = 6 + 2√3 кв.дм.

Объяснение:

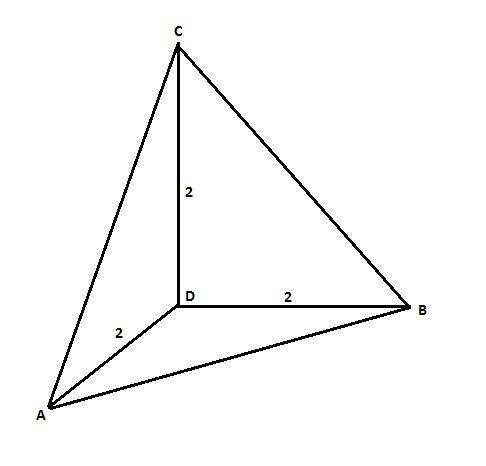
Смотрите рисунок.

Каждая из граней на боковой поверхности - это прямоугольный равнобедренный треугольник.

Катеты у них по условию равны:

AD = BD = CD = 2 дм, значит, гипотенузы:

AB = AC = BC = 2√2 дм.

Площадь боковой поверхности равна трем площадям треугольников, площадь каждого из которых равна половине произведения катетов:

S(бок) = 3*a*b/2 = 3*2*2/2 = 6 кв.дм.

Основание - равносторонний треугольник со стороной d = 2√2 дм.

Площадь основания:

S(осн) = d^2*√3/4 = (2√2)^2*√3/4 = 8*√3/4 = 2√3 кв.дм.

Площадь полной поверхности:

S(полн) = S(бок) + S(осн) = 6 + 2√3 кв.дм.