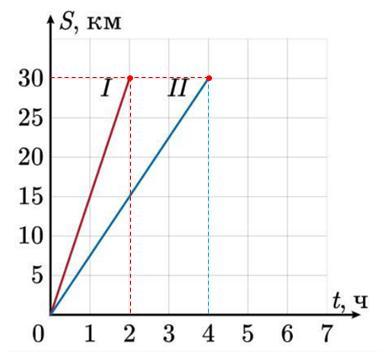
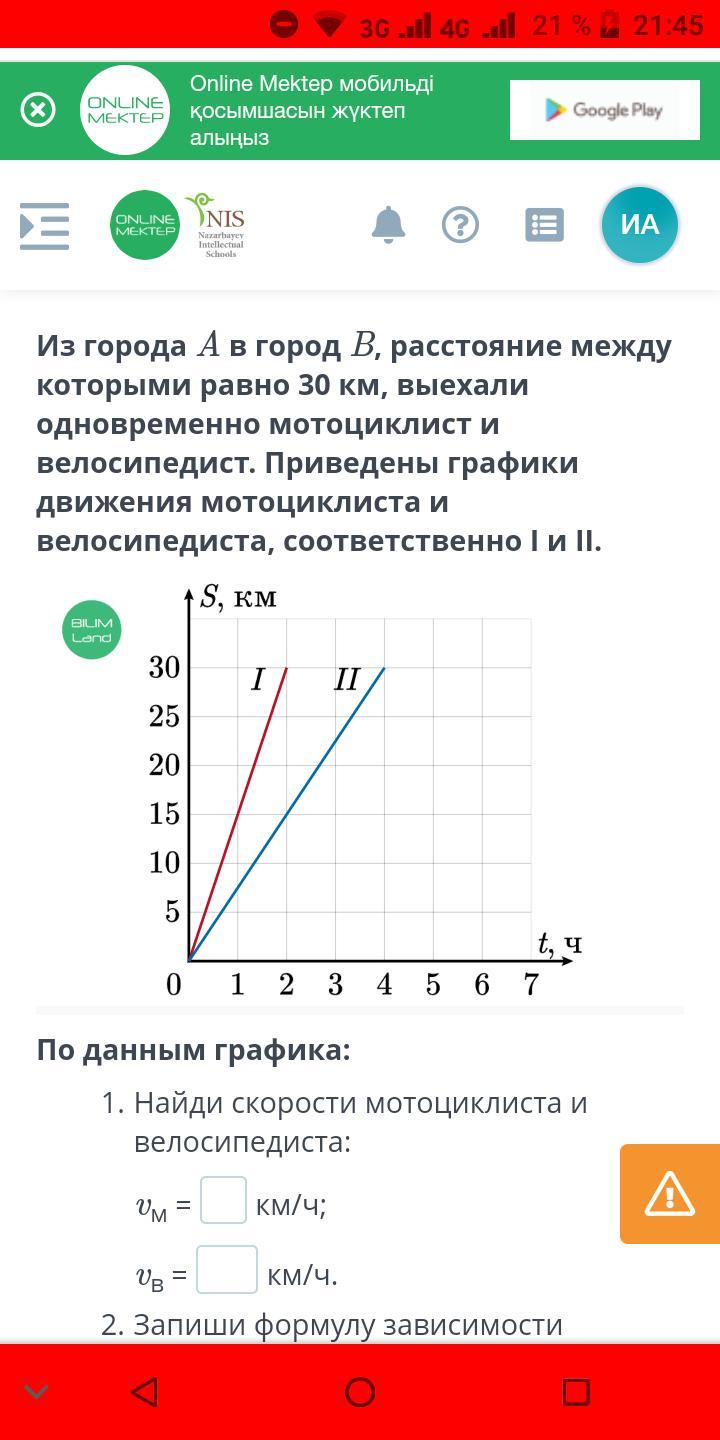
Из города A в город B, расстояние между которыми равно 30 км, выехали одновременно мотоциклист и велосипедист. Приведены графики движения мотоциклиста и велосипедиста, соответственно I и II. По данным графика: Найди скорости мотоциклиста и велосипедиста: vм = 15 км/ч; vв = 7,5 км/ч. Запиши формулу зависимости пройденного пути мотоциклиста от времени. Sм = t. Запиши формулу зависимости пройденного пути велосипедиста от времени. Sв = t. На сколько часов раньше прибыл в город B мотоциклист, чем велосипедист? 2 ч.
Ответы
Ответ:
Скорость мотоциклиста υм = 15 км/ч
Скорость велосипедиста υв = 7,5 км/ч
Формула зависимости пройденного пути мотоциклиста от времени
Sм = 15·t
Формула зависимости пройденного пути велосипедиста от времени
Sв = 7,5·t
Мотоциклист прибыл в город B на 2 часа раньше велосипедиста
Пошаговое объяснение:
Нужно знать:
Пройденный путь S объекта определяется через скорость υ и время t по формуле: S = υ · t (1).
Из этой формулы получим зависимость скорости υ от пройденного пути S и от времени t:
υ = S / t (2).
Решение.
По графику определяем (см. рисунок):
1) мотоциклист прибыл в город B через tм = 2 часа (красная штриховка);
2) велосипедист прибыл в город B через tв = 4 часа (синяя штриховка).
Так как пройдённый мотоциклистом и велосипедистом равен
Sм = Sв = 30 км,
то по формуле (2) находим скорость
а) мотоциклиста υм = Sм / tм = 30/2 = 15 км/ч.
б) велосипедиста υв = Sв / tв = 30/4 = 7,5 км/ч.
Из формулы (1) получим формулы зависимости пройденного пути от времени:
в) мотоциклист Sм = υм · t = 15·t;
г) велосипедист Sв = υв · t = 7,5·t.
Из заключений 1) и 2) получим:
д) мотоциклист прибыл в город B на
t = tв - tм = 2 часа
раньше велосипедиста.