Предмет: Математика,
автор: 90059
Вычислите производную функции
Приложения:
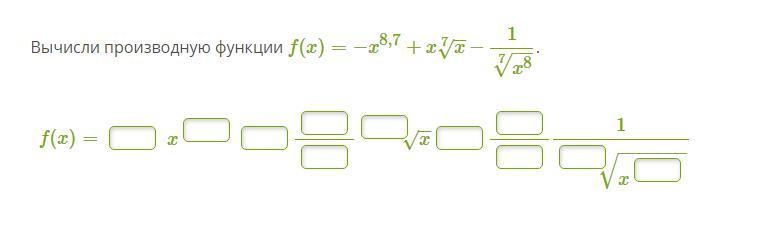
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: nadtochaeva2014
Предмет: Английский язык,
автор: лиза1730
Предмет: Русский язык,
автор: Anastasiya6643
Предмет: Музыка,
автор: KGLiza06
Предмет: Математика,
автор: Ксения20081