Предмет: Геометрия,
автор: ksyshadoroh
Радиус круга, описанного вокруг правильного многоугольника равняется 4см, а радиус круга, вписанного в этот многоугольник 2V2. Найти количество сторон этого многоугольника.
Ответы
Автор ответа:
1
Правильный многоугольник имеет вписаную и описанную окружности, их центры совпадают.
То есть центр правильного многоугольника одновременно является пересечением биссектрис углов и серединных перпендикуляров к сторонам.
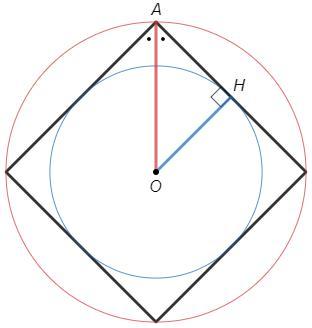
Проведем радиус вписанной окружности OH, ∠H=90°
Проведем радиус описанной окружности OA, ∠OAH=∠A/2
sin(A/2) =sin(OAH) =OH/OA =r/R =2√2/4 =1/√2
=> ∠A/2 =45° => ∠A=90°
Понятно, что данный многоугольник - квадрат, 4 стороны.
n =360°/(180°-ф) =360°/(180°-90°) =4
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Aliya19791
Предмет: Английский язык,
автор: tmarieva
Предмет: Русский язык,
автор: KURMANTAEVA
Предмет: Математика,
автор: maks2485