Предмет: Геометрия,
автор: NaziNavi
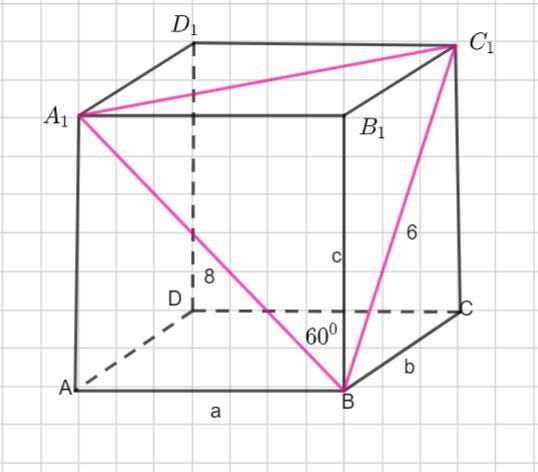
Найдите объем прямоугольного параллелепипеда в котором диагонали боковых граней, выходящих из одной вершины, равны 6 и 8, а угол между ними 60°
Подсказка: тут нужно решить через систему
Ответы
Автор ответа:
3
Ответ:
Объем прямоугольного параллелепипеда равен 48 √5 куб. ед.
Объяснение:
По условию задан прямоугольный парллелепипед. Пусть его измерения a, b,c .
Рассмотрим Δ
AB =a,
Воспользуемся теоремой Пифагора и составим уравнение
Рассмотрим Δ
Получим уравнение, используя теорему Пифагора
Из Δ
Рассмотрим Δ и применим теорему косинусов: квадрат любой стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Тогда получим третье уравнение
Значит, можно составить систему:
Сложим почленно все три уравнения и получим
Если ,
, то
Если и
то
Если и
то
Объем прямоугольного параллелепипеда определяется по формуле:
куб. ед.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: vikoshka1405
Предмет: Английский язык,
автор: elinaizabakarowа
Предмет: Русский язык,
автор: Elizavetta1112
Предмет: Алгебра,
автор: londorom