Предмет: Алгебра,
автор: Iskandarmad81
помогите срочно заранее спасибо нужно только 2-ой
Приложения:
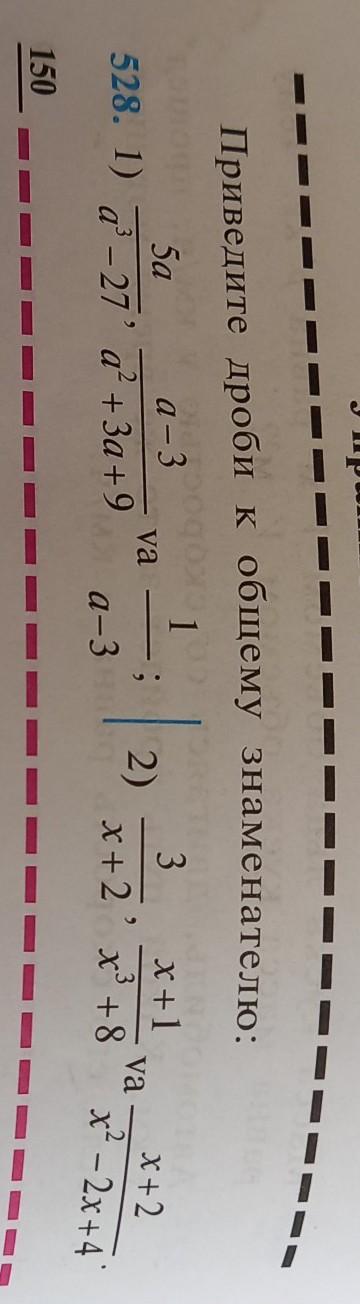
Ответы
Автор ответа:
0
Объяснение:
.
Автор ответа:
0
Объяснение:
х³+8= (х+2)(х-2)²;
х²-2х+4= (х-2)²
Приложения:
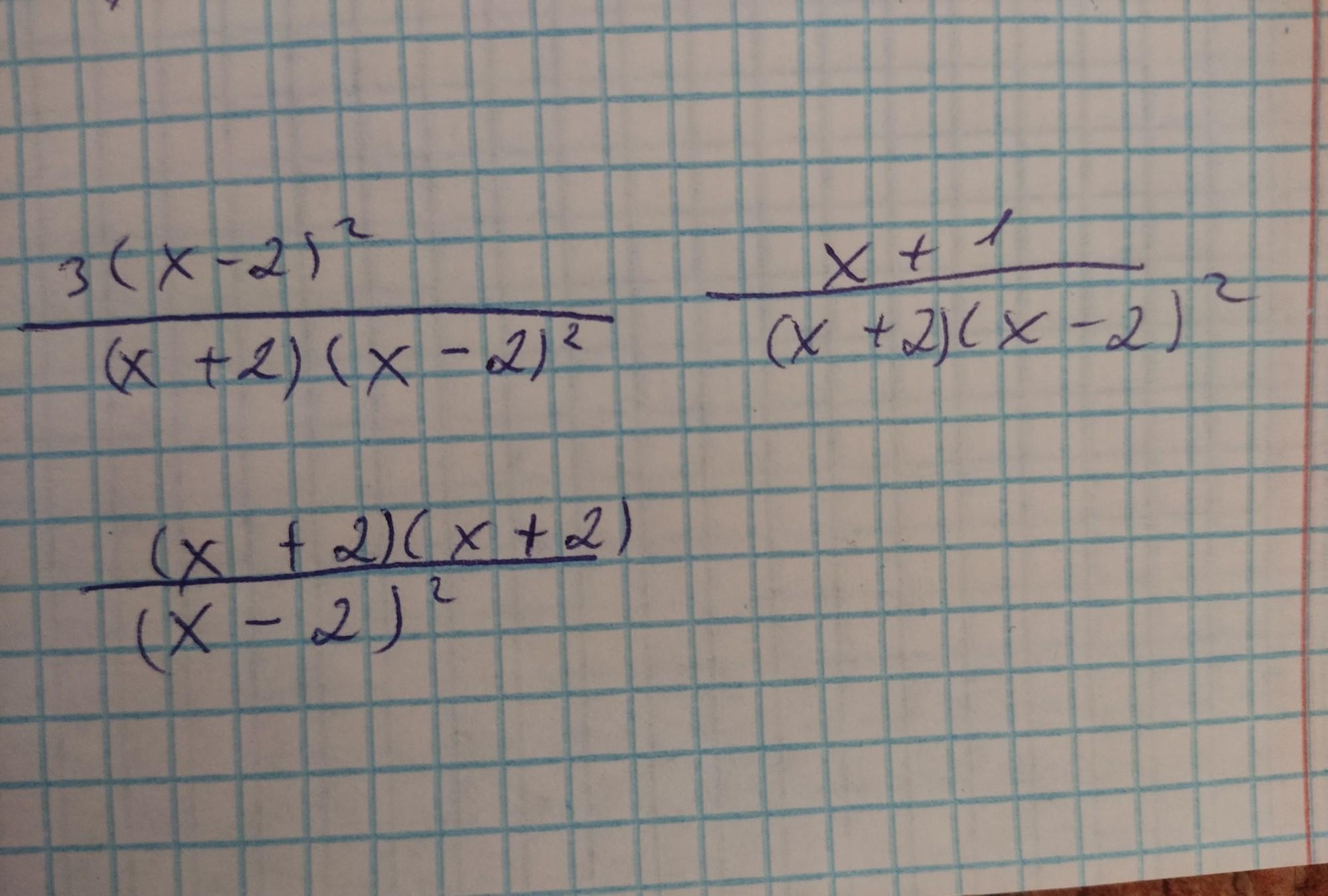
Похожие вопросы
Предмет: Английский язык,
автор: vjj2лд
Предмет: Русский язык,
автор: haza55
Предмет: Русский язык,
автор: vipkoraleva
Предмет: Математика,
автор: seredinaekater