Предмет: Математика,
автор: Aleksandr11233211
Помогите, пожалуйста, нужно решить дифференциальные уравнения первого и второго порядка:
Приложения:
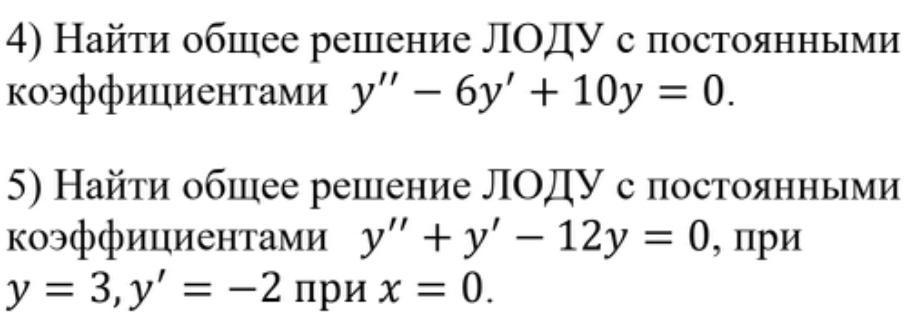
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Мартигже
Предмет: Английский язык,
автор: Martina17
Предмет: Русский язык,
автор: Pinkamina585585
Предмет: Литература,
автор: hellllo15
Предмет: Математика,
автор: beket2005