Question

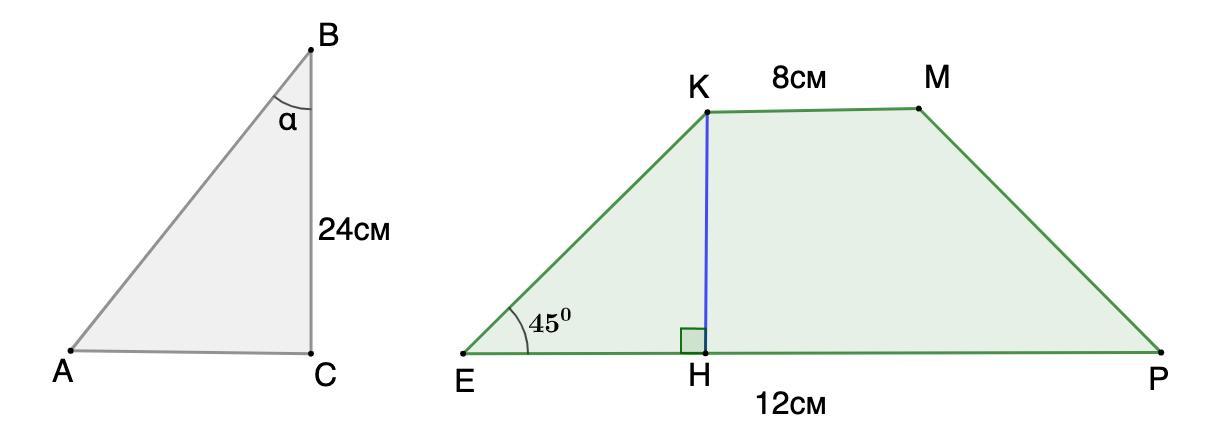
У прямокутному трикутнику один із катетів дорівнює 24см, тангенс
прилеглого кута дорівнює 3/4. Знайти другий катет і гіпотенузу

Основи ріОснови рівнобічної трапеції дорівнюють 8см і 12см, а кут при основі
дорівнює 450. Знайти висоту та бічну сторону трапеціївнобічної трапеції дорівнюють 8см і 12см, а кут при основі дорівнює 450. Знайти висоту та бічну сторону трапеції
Решение нужно к воскресению , даю 40 баллов !

Answer 1

Ответ:

1) Второй катет треугольника равен 18 см, гипотенуза равна 30 см.

2) Высота трапеции равна 2 см, боковая сторона равна 2√2 см.

Объяснение:

1) В прямоугольном треугольнике один из катетов равен 24см, тангенс прилежащего угла равен 3/4. Найти второй катет и гипотенузу.

2) Основания равнобочной трапеции равны 8см и 12см, а угол при основании равен 450. Найти высоту и боковую сторону трапеции.

1) Дано: ΔАВС - прямоугольный;

ВС = 24 см;

tg α = 3/4

Найти: АВ; АС.

Решение:

• Тангенс угла α - отношение противолежащего катета к прилежащему.

$\displaystyle tg\;\alpha = \frac{AC}{BC} \\\\\frac{3}{4}=\frac{AC}{24} \\\\AC=\frac{3\cdot24}{4}=18\;_{(CM)}$

Гипотенузу можем найти по теореме Пифагора:

АВ² = ВС² + АС²

АВ² = 576 + 324 = 900

АВ = √900 = 30 (см)

Второй катет треугольника равен 18 см, гипотенуза равна 30 см.

2) Дано: ЕКМР - равнобочная трапеция;

КН - высота;

КМ = 8 см; ЕР = 12 см; ∠Е = 45°;

Найти: КН, ЕК.

Решение:

1. Рассмотрим ЕКМР - равнобочную трапецию.

• В равнобедренной трапеции высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшая из которых равна полуразности оснований.

⇒ ЕН = (ЕР - КМ) : 2 = (12 - 8) : 2 = 2 (см)

2. Рассмотрим ΔЕКН - прямоугольный.

∠Е = 45°

$\displaystyle tg\angle{E}= \frac{KH}{EH}\\ \\tg\;45^0 = 1\\\\\frac{KH}{2}=1\\ \\KH = 2 \;_{(CM)}$

Боковую сторону можем найти по теореме Пифагора:

ЕК² = ЕН² + НК²

ЕК² = 4 + 4 = 8

ЕК = √8 = 2√2 (см)

Высота трапеции равна 2 см, боковая сторона равна 2√2 см.