Предмет: Алгебра,
автор: igor2008test
Помогите 1 задание, скрин прикрепил
Приложения:
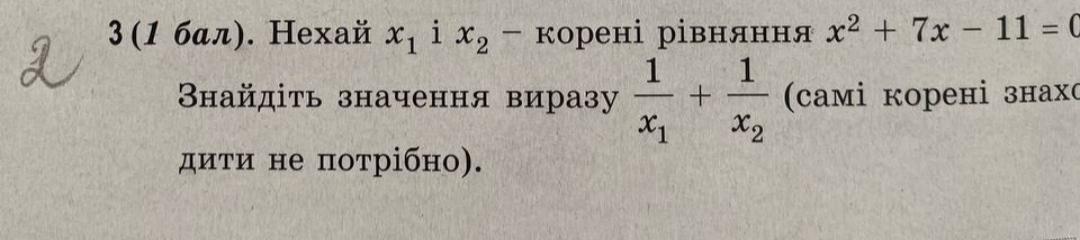
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Если и
корни квадратного уравнения
Не решая квадратное уравнение, найдем значение выражения
Для квадратного уравнения , если
и
корни квадратного уравнения, то по теореме Виета сумма корней приведенного квадратного уравнения равна коэффициенту при х, взятому с противоположным знаком, а произведение корней равно свободному члену.
Тогда найдем значение выражения, предварительно преобразовав его.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: 2002Григорий2002
Предмет: Окружающий мир,
автор: kirill313212
Предмет: Английский язык,
автор: ayana0309
Предмет: Математика,
автор: Uliana651