Question

Помогите пожалуйста.

В выпуклом четырёхугольнике ABCD диагональ AC образует со сторонами BC и CD углы, соответственно равные 78° и 75°. Найдите угол BDC, если AB = AC = AD. Ответ дайте в градусах​

Answer 1

Ответ:

12°

Объяснение:

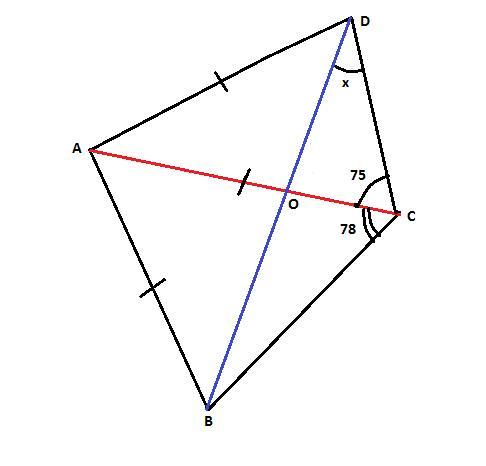
Смотрите рисунок. 4-угольник ABCD выглядит примерно так.

AB = AC = AD, ∠ACD = 75°, ∠ACB = 78°.

Нужно найти угол BDC = x°.

Решение:

Треугольники ABC и ACD - равнобедренные.

∠ACD = ∠ADC = 75°, ∠CAD = 180° - 75° - 75° = 30°.

∠ACB = ∠ABC = 78°, ∠BAC = 180° - 78° - 78° = 24°.

∠BAD = ∠BAC + ∠CAD = 30° + 24° = 54°

Треугольник BAD - тоже равнобедренный, и угол при вершине:

∠BAD = 54°

Значит, остальные углы при основании равны друг другу:

∠ADB = ∠ABD = (180° - 54°)/2 = 126°/2 = 63°

∠BDC = x° = ∠ADC - ∠ADB = 75° - 63° = 12°