Предмет: Геометрия,
автор: kdvflm
Задание 4 (25 баллов).
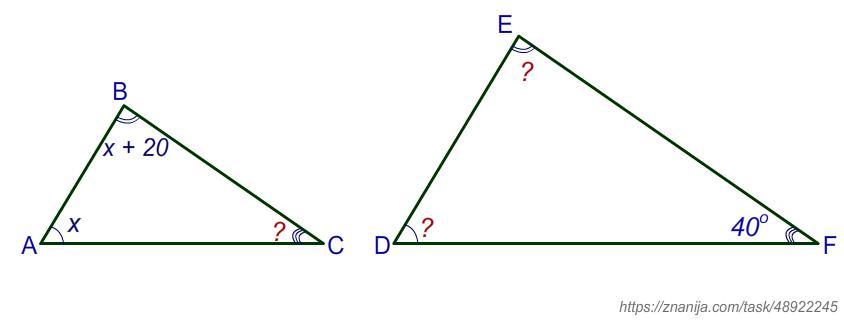
ΔABC ∼ ΔDEF. ∠В – ∠А = 20°. ∠F = 40°. Найдите углы D, E и С.
Ответы
Автор ответа:
15
Ответ:
∠D = 60°; ∠E = 80°; ∠C = 40°.
Объяснение:
Даны подобные треугольники ΔABC и ΔDEF. Разность углов ∠В – ∠А = 20°, ∠F = 40°. Найти углы D, E и С.
Дано:
ΔABC ∼ ΔDEF;
∠В – ∠А = 20°;
∠F = 40°.
Найти: ∠D, ∠E, ∠С.
Решение.
- Подобные треугольники - это треугольники, у которых соответствующие углы равны, соответствующие стороны пропорциональны.
1) По условию ΔABC ∼ ΔDEF.
Тогда
∠A = ∠D;
∠B = ∠E;
∠C = ∠F = 40°.
2) Условие ∠В – ∠А = 20° обозначает, что ∠B больше, чем ∠A на 20°.
Пусть ∠A = x, тогда ∠B = x + 20°.
- Сумма углов в треугольнике равна 180°.
В ΔABC:
∠A + ∠B + ∠C = 180°;
x + x + 20° + 40° = 180°;
2x = 120°;
x = 60°.
∠A = 60°; ∠B = 60° + 20° = 80°.
3) В подобных треугольниках соответствующие углы равны.
∠D = ∠A = 60°;
∠E = ∠B = 80°.
Таким образом, ∠D = 60°; ∠E = 80°; ∠C = 40°.
#SPJ1
Приложения:
zhenialarina3:
Спасибо огромное! Замечательный ответ! Вы мне очень помогли.
Отличный ответ, всё понятно, спасибо вам большое^
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Английский язык,
автор: Ытачы
Предмет: Русский язык,
автор: никмир1
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: danilmtv2066