Предмет: Геометрия,
автор: Gsshsj
❗❗❗❗СРОЧНО ❗❗❗❗
Точка О - центр кола, вписаного в трикутник АВС. <А=40 градусів, <В=58 градусів. Знайдіть <ОАС, <ОВС, <ОСА.
7 КЛАСС
МОЖЕТЕ ПОЖАЛУЙСТА С РИСУНКОМ!
Ответы
Автор ответа:
1
Ответ:
∠OAC = 20°, ∠OBC = 29°, ∠OCA =41 °
Объяснение:
1) Рассмотрим 2 треугольника: AOL и AOH. OH = OL, так как это радиусы окружности. AL = AH, так как это касательные к окружности, которые были проведены из одной точки A. AO - общая сторона, она одинакова для двух треугольников. Из этого всего можно сделать вывод, что треугольник AOL и AOH равны по 3 сторонам.
Если треугольники равны, то и равны их углы. ∠LAO = ∠OAC = 20°
2) Та же история. ∠OBC = ∠OBA = 29°
3) ∠C = 180° - (58° + 40°) = 82°. Далее всё так же, как и в случае 1). ∠OCA = ∠OCB = 41°
Ответ: 1) 20° 2) 29° 3) 41°
Приложения:
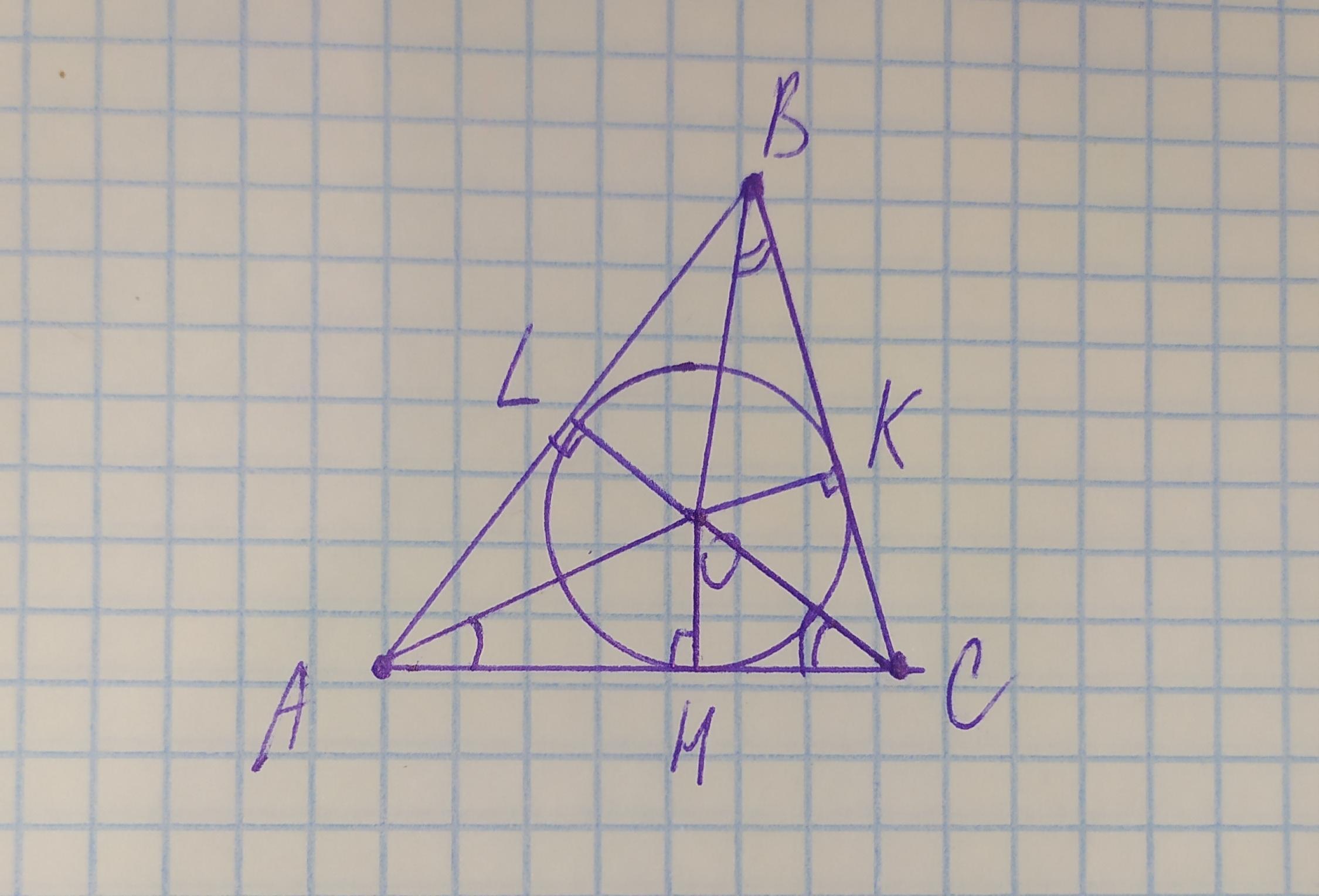
Gsshsj:
спасибо
не за что)
Похожие вопросы
Предмет: Русский язык,
автор: moxito1704
Предмет: Русский язык,
автор: tpolozova1972
Предмет: Русский язык,
автор: татьяна648
Предмет: Русский язык,
автор: vadf2
Предмет: Қазақ тiлi,
автор: MichaelEirich