Предмет: Геометрия,
автор: zigacevevgenij77
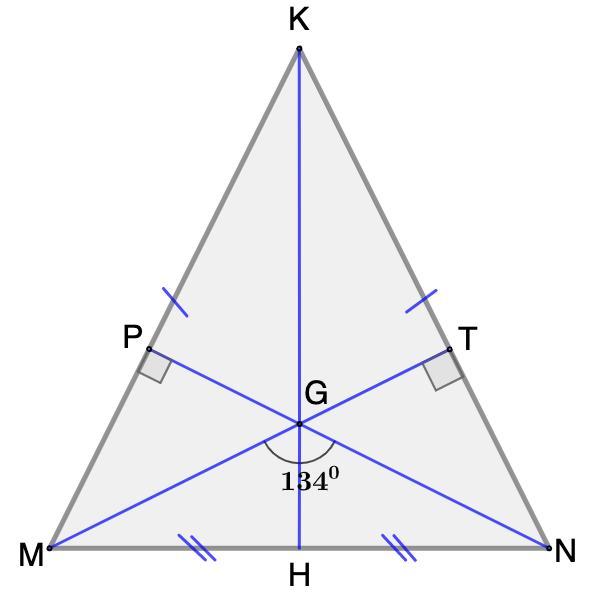
Высоты MT и NP равнобедренного ∆ MKN с основанием MN пересекаются в точке G найди градусную меру угла GKN если угол MGN=134°
Ответы
Автор ответа:
6
Ответ:
Градусная мера угла GKN равна 23°.
Объяснение:
Высоты MT и NP равнобедренного ∆MKN с основанием MN пересекаются в точке G.
Найти градусную меру угла GKN, если угол MGN=134°.
Дано: ∆MKN - равнобедренный.
MT и NP - высоты;
MT ∩ NP = G;
∠MGN=134°.
Найти: ∠GKN.
Решение:
1. Рассмотрим ∆MKN - равнобедренный.
- Высоты треугольника пересекаются в одной точке.
MT и NP - высоты ⇒ КН - высота.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
⇒ КН - высота, медиана, биссектриса.
MH = HN.
2. Рассмотрим ΔMGN.
GH - высота.
MH = HN (п.1)
⇒ GH - медиана.
- Если в треугольнике высота является медианой, то треугольник равнобедренный.
ΔMGN - равнобедренный.
⇒ GH - биссектриса.
∠MGH = ∠HGN = 134° : 2 = 67°
3. Рассмотрим ΔGKT - прямоугольный.
- Вертикальные углы равны.
⇒ ∠MGH = ∠KGT = 67°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠GKN = 90° - ∠KGT = 90° - 67° = 23°
Градусная мера угла GKN равна 23°.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: танюшка557
Предмет: Русский язык,
автор: azizanis60
Предмет: Другие предметы,
автор: nata0984
Предмет: Українська мова,
автор: nebor20021
Предмет: Английский язык,
автор: Sasanan