Предмет: Математика,
автор: aleksmishkova
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Приложения:
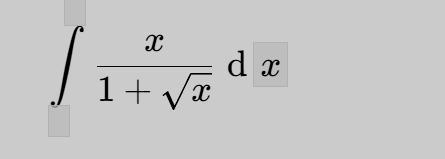
Ответы
Автор ответа:
0
Ответ:
Метод замены переменной .
Похожие вопросы
Предмет: Русский язык,
автор: tanja07061987
Предмет: Русский язык,
автор: mcndbdhdjshdh
Предмет: Окружающий мир,
автор: АртёмБардыгин
Предмет: Русский язык,
автор: aru5697