Предмет: Математика,
автор: milkyway5132
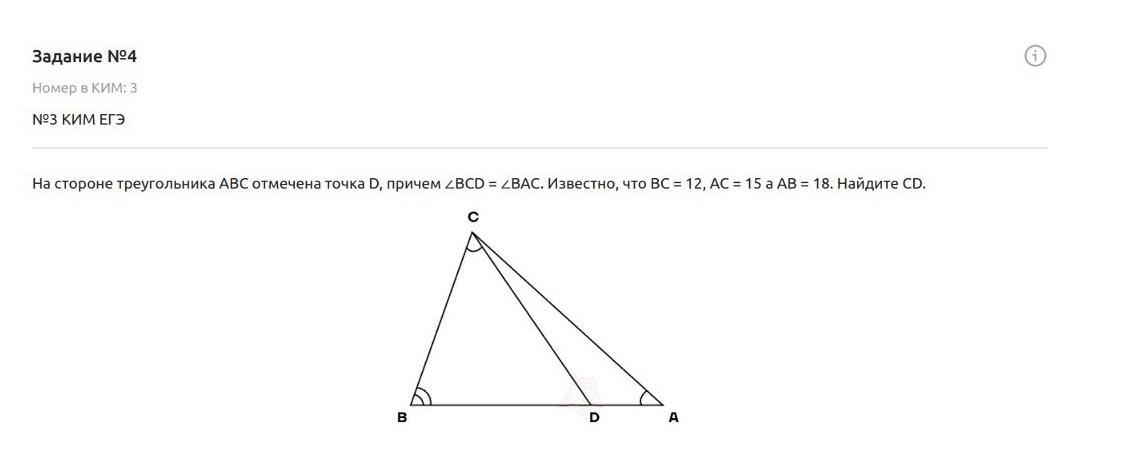
на стороне треугольника ABC отмечена точка D, причём углы BCD = BAC. Инзвестно, что BC = 12, AC =15, AB = 15. Найдите CD.
Приложения:
Ответы
Автор ответа:
2
Ответ:
CD =10 ед.
Пошаговое объяснение:
Рассмотрим рисунок. На рисунке дан ΔАВС,
причем ∠ВСD = ∠ВАС.
BC =12, AC =15, AB =18
Найдем CD .
Рассмотрим Δ ВСD и ΔВАС и докажем, что они подобны .
∠BCD= ∠BAC по условию и ∠В - общий. Тогда треугольники подобны по двум углам. Из подобия треугольников следует пропорциональность соответствующих сторон. Составим пропорцию
Похожие вопросы
Предмет: Русский язык,
автор: kudinkaelenka
Предмет: Русский язык,
автор: часодей1
Предмет: Английский язык,
автор: КристинаГерГерГер
Предмет: Математика,
автор: raida14
Предмет: История,
автор: Аноним