Предмет: Геометрия,
автор: handziiarsenii
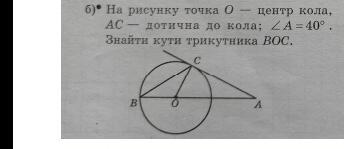
На рисунку точка О центр кола. AC - дотична до кола: 2А -40° 2 = Знайти кути трикутника ВОс.
Приложения:
Ответы
Автор ответа:
2
Відповідь:
Пояснення:
розв'язання завдання додаю
Приложения:

Автор ответа:
1
Ответ:
уголСОВ=130°
уголСВО=уголВСО=25°
Объяснение:
Дано:
О - центр окружности
СА-касательная
угол А=40°
Найти: угол BOC
Решение:
1) СА касается окружности в т. С, а СО-радиус=> радиус, проведённый в точку касания равен 90°
угол ОСА=90°
2) Р/см треугольник СОА - прямоугольный; угол СОА=90°-40°=50°
3) угол СОА и угол ВОС - смежные=> угол СОА+угол ВОС=180° => уголВОС=180°-уголСОВ=180°-50°=130°
4) Треугольник ВОС - равнобедренный, так как ВО=ОС(радиусы) => уголСВО=уголВСО=(180°-130°)÷2=25°
Ответ: уголСОВ=130°, уголСВО=уголВСО=25°
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: данила20043
Предмет: Русский язык,
автор: marina55812
Предмет: Другие предметы,
автор: mishaeysiev
Предмет: Русский язык,
автор: ILYANETYLKO