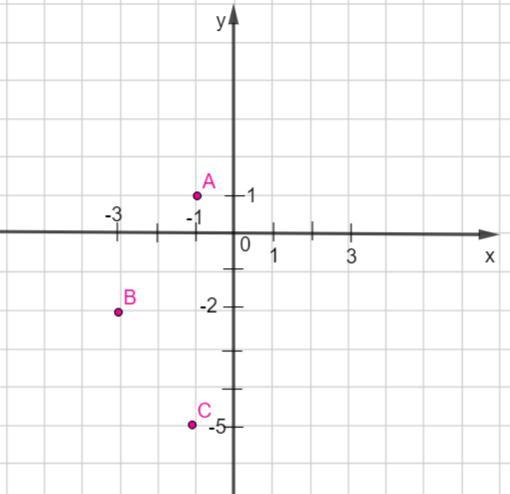
Дан треугольник АВС, где А(-1;1) В(-3;-2) С(-1;-5) постройте точку В1, симметричную точке В относитеньно прямой АС, и укажите координаты точки В1
ПОЖАЛУЙСТА, ЭТО СРОЧНО!!!
Ответы
Ответ:
Точка , симметричная точке В относительно прямой АС имеет координаты
Объяснение:
По условию задан Δ АВС
А( -1; 1), В(-3; -2), С (-1; -5)
Построим систему координат и отметим эти точки ( показано на первом рисунке)
Соединим построенные точки отрезками и построим треугольник ΔАВС. По рисунку видно, что полученный треугольник равнобедренный. Докажем это. По формуле расстояния между точками найдем длины боковых сторон АВ и ВС .
Пусть даны точки
Тогда расстояние между ними определяется по формуле
Тогда длины сторон
Так как АВ = ВС, то треугольник равнобедренный с основанием АС.
Симметрией относительно прямой а или осевой симметрией называется преобразование переводящее точку А в точку так, что а - серединный перпендикуляр к отрезку
Тогда построим прямую АС. По условию эта прямая ось симметрии.
Проведем высоту ВН треугольника Δ АВС. Так как треугольник АВС равнобедренный, то высота , проведенная к основанию является медианой и точка Н - середина основания. Найдем координаты точки Н
H(-1; -2)
Длина высоты ВН равна 2. Докажем это по формуле расстояния между точками.
Отметим точку на продолжении высоты ВН на расстоянии 2 единицы от точки Н. Полученная точка имеет координаты
.