Предмет: Алгебра,
автор: katkoski97
Помогите решить пожалуйста. Расписывайте прям понятно
Приложения:
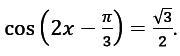
Simba2017:
2x-pi/3=+-pi/6+2pik
a)2x=pi/6+pi/3+2pik=pi/2+2pik; x=pi/4+pik
б)2x=-pi/6+pi/3+2pik=pi/6+2pik;x=pi/12+pik
Спасибо большое!)
А что значит а и б?
два случая рассмотрела каждый отдельно..
в первом 2x=pi/6+.... во втором 2x=-pi/6+...
Спасибо!!А мне тогда тоже лучше два отдельно написать?Или только один, как думаете?
в решении пишите по отдельности, но в ответе указывайте обы значения
спасибо!
Ответы
Автор ответа:
1
Ответ:
Если , то
.
Ответ: или
Похожие вопросы
Предмет: Английский язык,
автор: gggvp2173
Предмет: Другие предметы,
автор: окружаюшиймир7
Предмет: Окружающий мир,
автор: Tortik230
Предмет: Биология,
автор: uliamilovanova