Предмет: Математика,
автор: nazarijzakrevskij
найти производную функции
Приложения:
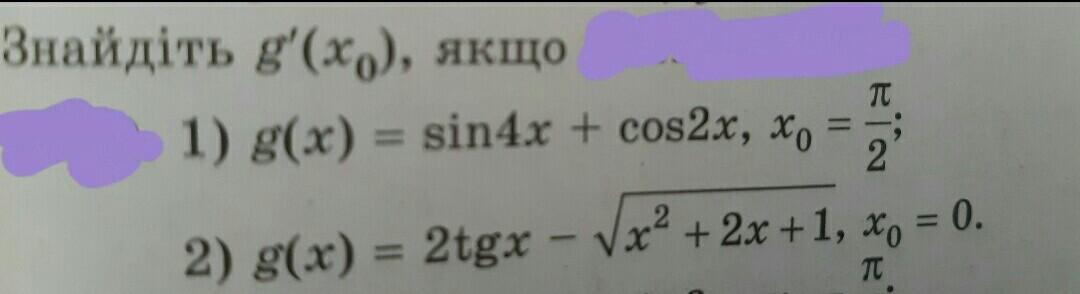
Ответы
Автор ответа:
1
1) g'(x)=4cos4x-2sin2x
g'(π/2)=4cos(4π/2)-2sin(2*π/2)=4cos(2π)-2sin(π)=4*1-2*0=4;
2) g'(x)=2/(сos²x)-(1/(2√(x²+2x+1))*( x²+2x+1)'=2/(сos²x)-(2x+2)/(2√(x²+2x+1))=
2/(сos²x)-(x+1)/√(x²+2x+1);
g'(0)=2/(сos²0)-(0+1)/√(0²+2*0+1)=2-1=1;
используемые формулы
(sinkx)'=k*coskx
(coskx)'=-k*sinkx
(√u)'=(1/(2√u))*u'
(tgx)'=1/cos²x
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Английский язык,
автор: anaskyx
Предмет: Русский язык,
автор: тата213
Предмет: Математика,
автор: aleksangra900