Предмет: Математика,
автор: mainkravt15
Найдите cosx, если sin x = -0,8, п/2
Приложения:
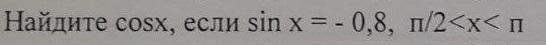
Ответы
Автор ответа:
0
Ответ:
-0,6
Пошаговое объяснение:
Определяем знак:
x лежит во второй координатной четверти, поэтому косинус принимает отрицательные значения
Похожие вопросы
Предмет: Английский язык,
автор: iergabyl03
Предмет: Английский язык,
автор: Padry
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Djksksk
Предмет: Қазақ тiлi,
автор: amertatch