ПОМОГИТЕ МИЛЫЕ!!!!
В ромбе MNAB точки G , H , K и L являются серединами его сторон. Чему равен периметр четырёхугольника GHKL , если диагонали ромба равны 245, 7 см и 387,9 см?
Ответы
Ответ:
6,336
Стороны четырехугольника GHKL - средние линии треугольников.
0 / 0
Ответ:
633,6см
Пошаговое объяснение:
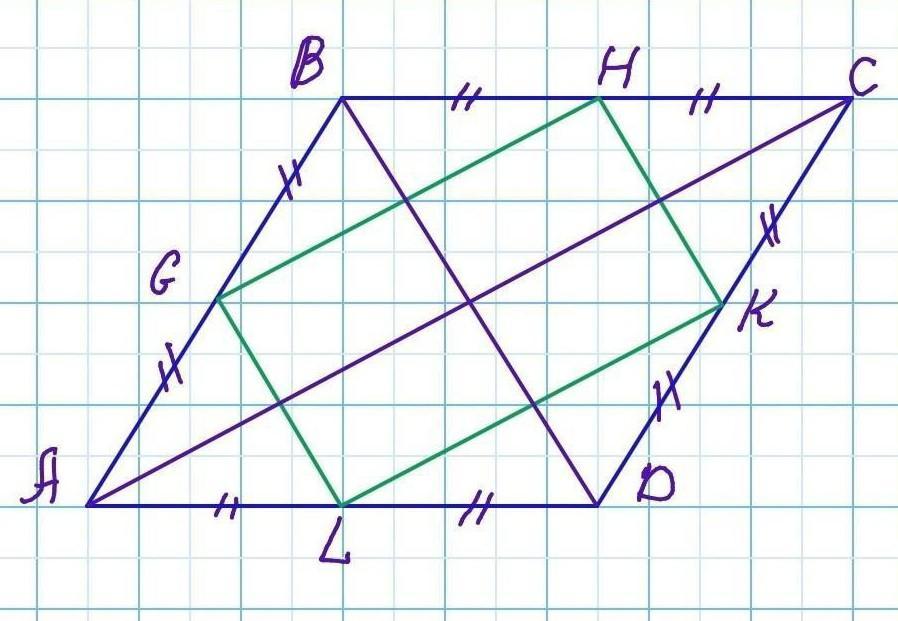
В условии неправильно указаны буквы, поэтому обозначим ромб как ABCD.(Мне так удобнее)
Дано: ABCD - ромб. AB=BC=CD= AD. Так как G,H,K и L являются серединами сторон ромба, то AG=GB=BH=HC=CK=KD=DL=AL. Диагональ АС = 245,7 см, диагональ BD = 387,9 см.
Найти: Р(GHKL)
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороны.
GH - средняя линиия △ABC. GH= ½ × АС;
LK - средняя линиия △ACD. LK= ½ × АС;
KH - средняя линиия △BCD. KH= ½ × BD;
GL - средняя линиия △ABD. GL= ½ × BD;
Периметр четырёхугольника - это сумма всех его сторон.
Р(GHKL) = GH+LK+KH+GL= ½ × АС + ½ × АС + ½ × BD + ½ × BD = AC+BD = 245,7+387,9 = 633,6см