Предмет: Математика,
автор: wqeew21
Вычислите определенный интеграл используя методом интегрирования!
Помогите пожалуйста
Приложения:
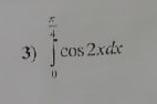
Ответы
Автор ответа:
1
Ответ:
решение смотри на фотографии
Приложения:

Автор ответа:
0
Ответ:
1/2
Пошаговое объяснение:
ДЛЯ НАЧАЛА НАЙДЁМ НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ:
∫cos(2x)dx
СДЕЛАЕМ ЗАМЕНУ. ПОДСТАВИМ ДИФФЕРЕНЦИАЛ, ИСПОЛЬЗУЯ 1/t'*dt, ГДЕ t=2x И t'=2:
∫cos(2x)*1/2dt = ∫cos(2x)/2dt
ПОДСТАВИМ 2х=t:
∫cos(t)/2dt
ИСПОЛЬЗУЕМ СВОЙСТВО ИНТЕГРАЛА:
1/2*∫cos(t)dt
ИНТЕГРАЛ ОТ КОСИНУСА РАВЕН СИНУСУ:
1/2*sin(t)
ЗДЕЛАЕМ ОБРАТНУЮ ЗАМЕНУ t=2x:
1/2*sin(2x) = sin(2x)/2
ПОДСТАВИМ ПРЕДЕЛЫ ИНТЕГРИРОВАНИЯ ОТ 0 ДО pi/4 И ИСПОЛЬЗУЕМ ПРАВИЛО НЬЮТОНА-ЛЕЙБНИЦА:
sin(2*pi/4)/2-sin(2*0)/2
И ПРОСТО ВЫЧИСЛЯЕМ
Похожие вопросы
Предмет: Русский язык,
автор: vikasemkina7
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: qarayevaf
Предмет: Математика,
автор: zamirkazaly
Предмет: Математика,
автор: floridajim