докажите,что если основанием высоты пирамиды является центр вписанной в основание окружности,то двухграные углы,образованные боковыми гранями пирамиды с плоскостью основания равны
Ответы
Доказательство:
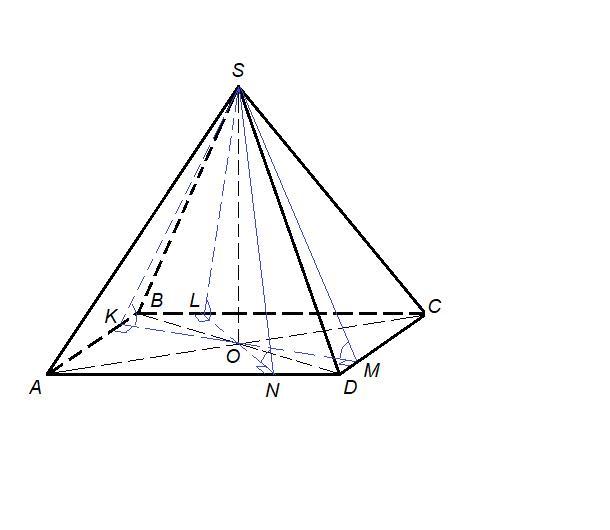
Рассмотрим четырехугольную пирамиду SABCD, в которой SO высота, О - центр окружности, вписанной в четырехугольник ABCD.
Проведем из точки О перпендикуляры к сторонам четырехугольника - радиусы в точки касания - OK⊥AB, OL⊥BC, OM⊥CD, ON⊥AD.
Отрезки OK, OL, OM, ON - проекции наклонных SK, SL, SM, SN на плоскость основания, значит
SK⊥AB, SL⊥BC, SM⊥CD и SN⊥AD по теореме о трех перпендикулярах.
Тогда ∠SKO, ∠SLO, ∠SMO и ∠SNO - линейные углы двугранных углов, образованных боковыми гранями пирамиды с плоскостью основания. Надо доказать их равенство.
ΔSOK = ΔSOL = ΔSOM = ΔSON по двум катетам:
- ∠SOK = ∠SOL = ∠SOM = ∠SON = 90°, так как SO - высота пирамиды;
- SO - общий катет;
- KO = LO = MO = NO как радиусы окружности.
Из равенства треугольников следует равенство углов:
∠SKO = ∠SLO = ∠SMO = ∠SNO.
Что и требовалось доказать.
Рассмотрена четырехугольная пирамида, но для любой другой пирамиды доказательство проводится аналогично.