Question

Знайдіть площу рівнобічної трапеції висота якої =10см, а кут між діагоналлю та нижньою основою дорівнює тридцять градусів.​

Answer 1

Ответ:

Площа трапеції дорівнює 100√3 см²

Пошаговое объяснение:

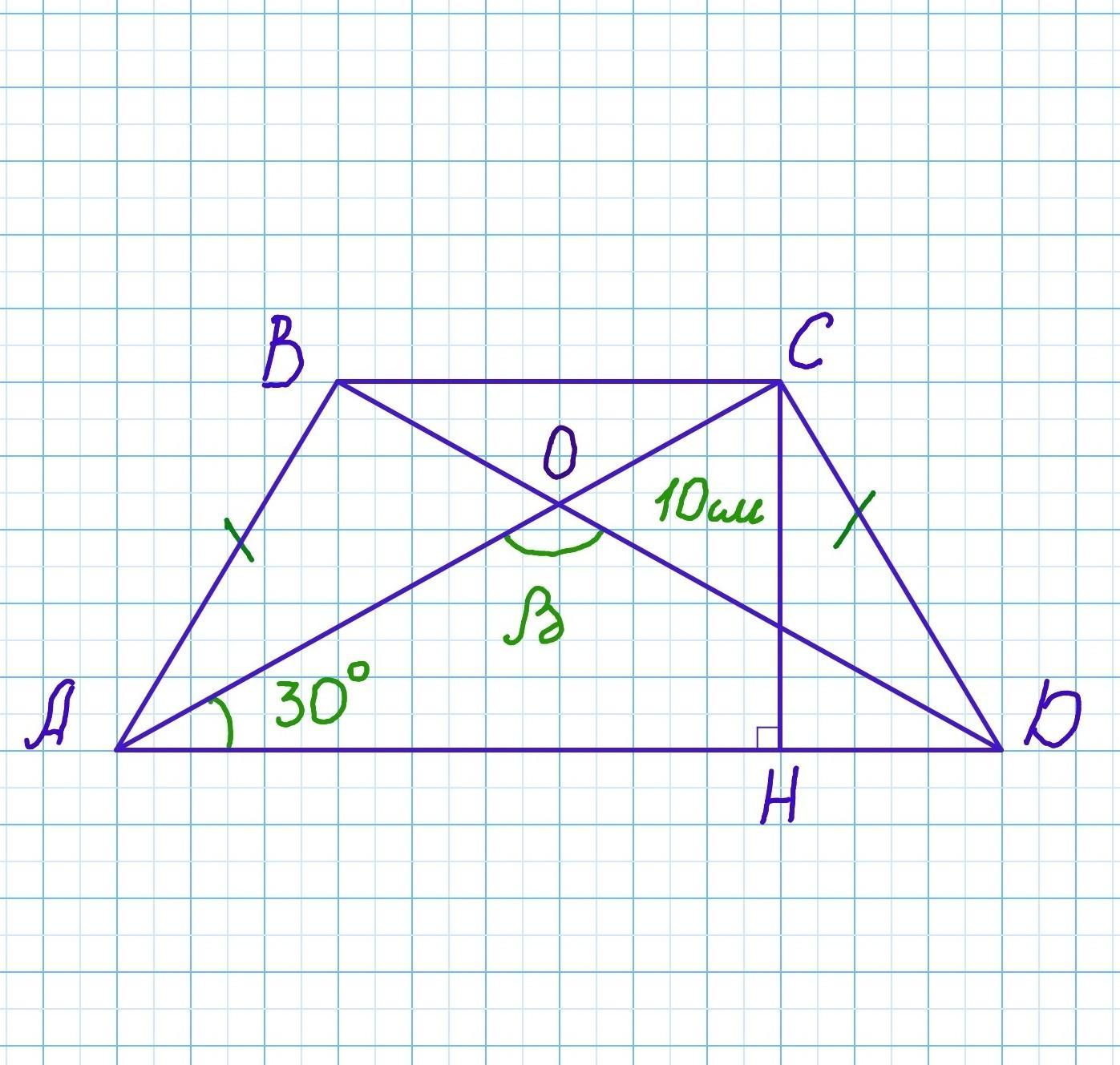
ABCD - рівнобічна трапеція. AB=CD. CH - висота, CH⟂AD, CH=10см.

Знайти: площу трапеції ABCD.

Рішення

1)Розглянемо прямокутний трикутник АСН(∠Н=90°).

• Катет, що лежить навпроти кута 30° дорівнює половині гіпотенузи.

Гіпотенуза АС=2•СН=2•10=20 см

2) Властивості рівнобічної трапеції:

• Діагоналі рівні: BD=AC=20 см;
• Однакові кути між діагоналями та основами: ∠CAD=∠BDA=30°

Так як сума кутів трикутника дорівнює 180°, то ∠АOD=180°-30°-30°=120°

3)Площа рівнобічної трапеції:

$S= \frac{1}{2} \times d_1 \times d_2 \times sin \beta = \frac{1}{2} \times 20 \times 20 \times sin120^\circ = 200 \times \frac{ \sqrt{3} }{2} = 100 \sqrt{3}$см².