Предмет: Геометрия,
автор: stasgumarru
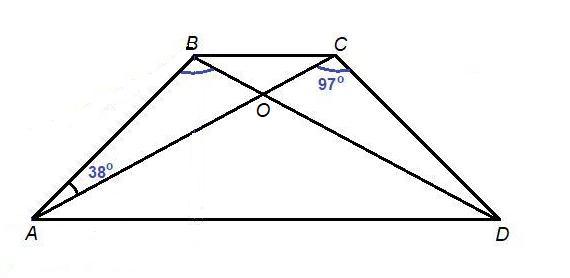
Найдите площадь равнобедренной трапеции,если известно, что её диагональ равная 6 см образует с боковыми сторонами углы 38° и 97°
Ответы
Автор ответа:
4
Ответ:
Площадь трапеции равна 9√2 см².
Объяснение:
ABCD - равнобедренная трапеция.
- В равнобедренной трапеции диагонали равны.
AC = BD = 6 см
∠ВАС = 38°, ∠ACD = 97° - углы, которые образует диагональ АС с боковыми сторонами.
ΔАВD = ΔDCA по трем сторонам:
- AB = CD, так как трапеция равнобедренная,
- BD = АС как диагонали равнобедренной трапеции,
- AD - общая сторона.
Тогда ∠ABD = ∠ACD = 97°.
Из ΔАОВ:
∠АОВ = 180° - (∠ОАВ + ∠ОВА) = 180° - (38° + 97°) = 180° - 135° = 45°
- Площадь четырехугольника можно найти как половину произведения диагоналей на синус угла между ними.
см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Мила14688900
Предмет: Українська мова,
автор: svyatoslavtsar
Предмет: Английский язык,
автор: kudrim1
Предмет: Литература,
автор: Mishka2014
Предмет: История,
автор: Аноним