Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить задачу
Приложения:
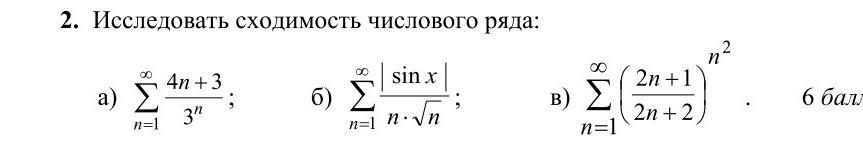
Ответы
Автор ответа:
2
Объяснение.
Применяем признак Даламбера
Ряд сходится
Так как при любом х, то подбираем мажорантный ряд
, который будет сходящимся, т.к. это обобщенный
гармонический ряд с показателем 3/2>1 .
Исходный функциональный ряд сходится при любом х ,
Применяем радикальный признак Коши.
Ряд сходится .
Похожие вопросы
Предмет: Русский язык,
автор: Лисоволк123
Предмет: Қазақ тiлi,
автор: BAKS1337
Предмет: Русский язык,
автор: ilyasokolov201
Предмет: Русский язык,
автор: bovk27101736
Предмет: Геометрия,
автор: HappyyAndrey