Предмет: Математика,
автор: richardreinerarp
Теория вероятности. Условие на приложении.
Приложения:
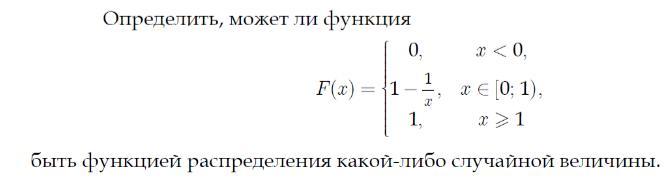
Ответы
Автор ответа:
1
Ответ: не может.
Пошаговое объяснение:
Функция распределения должна быть непрерывна во всех точках. А в данном случае функция F(x) имеет бесконечный разрыв в точке x=0. Действительно, так как выражение 1-1/x при x>0 и x⇒0 имеет своим пределом -∞, то "предел справа" функции F(x) в точке x=0 равен -∞, в то время как "предел слева" равен 0. Кроме того, так как функция распределения по своему определению есть вероятность, а вероятность не может быть отрицательной, то и функция распределения не может быть отрицательной. Между тем выражение 1-1/x в интервале (0;1) отрицательно. Поэтому функция F(x) не является функцией распределения какой-либо случайной величины.
Похожие вопросы
Предмет: Английский язык,
автор: диана1152
Предмет: Окружающий мир,
автор: СветлыйАнгел
Предмет: Русский язык,
автор: ulia47rys
Предмет: Литература,
автор: ablack13
Предмет: Окружающий мир,
автор: sergeev179p2x2i8