Предмет: Алгебра,
автор: alekseeva2019
решите неравенство (10x-x^2-24)log5(4sin^2 πx/2 +1) >= 1
Приложения:
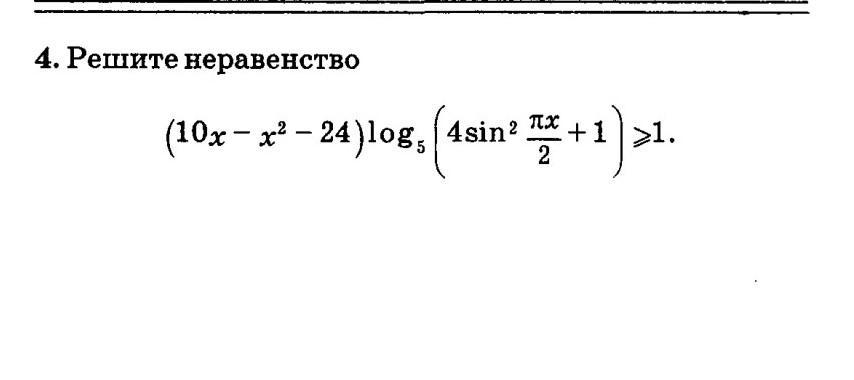
Ответы
Автор ответа:
3
Ответ:
Решение неравенства x ∈ { 5 }
Объяснение:
Дано неравенство:
Оценим множители слева по отдельности.
1) 10·x – x² – 24 = –(x² – 10·x) – 24 = –(x² – 10·x + 25 – 25) – 24 =
= –(x² – 2·5·x + 5²) + 25 – 24 = –(x – 5)² + 1 = 1 – (x – 5)² ≤ 1. Кроме того, 1 – (x – 5)² = 1 если только x = 5.
2) Так как | sinα | ≤ 1 для любого α∈R, то
следовательно
3) Применим следующее свойство логарифмической функции:
И тогда
причём равенство достигается если
Но это возможно, если
В вервом уравнении равенство достигается, если x = 5 (единственный корень). Подставим во второе уравнение и убедимся, что при x = 5 равенство достигается:
Значит, решением неравенства будет только x=5.
Похожие вопросы
Предмет: Русский язык,
автор: BlackElegant
Предмет: Русский язык,
автор: Максимка20161
Предмет: Английский язык,
автор: Vikusya2008
Предмет: Математика,
автор: nadezdamalaja
Предмет: Биология,
автор: zataevsaid