Предмет: Алгебра,
автор: Аноним
помогите пожалуйста (
Приложения:
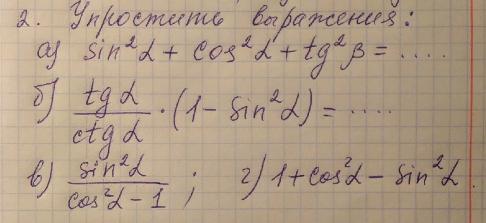
Аноним:
подробно пожалуйста
(((
а)1+tg^2(b)=(cos^2(b)+sin^2(b))/cos^2(b)=1/cos^2(b)
?//
Ответы
Автор ответа:
1
Объяснение:
фото.........
...
.......
Приложения:

Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: лол1068
Предмет: Қазақ тiлi,
автор: icemanfrost451
Предмет: Русский язык,
автор: zara127
Предмет: Информатика,
автор: matvey22829
Предмет: Математика,
автор: yasmin9090