Предмет: Алгебра,
автор: 123452622
5 Помогите пожалуйста !!!!!!!!
Приложения:
123452622:
черт не то задание закинул как поменять?
Ответы
Автор ответа:
1
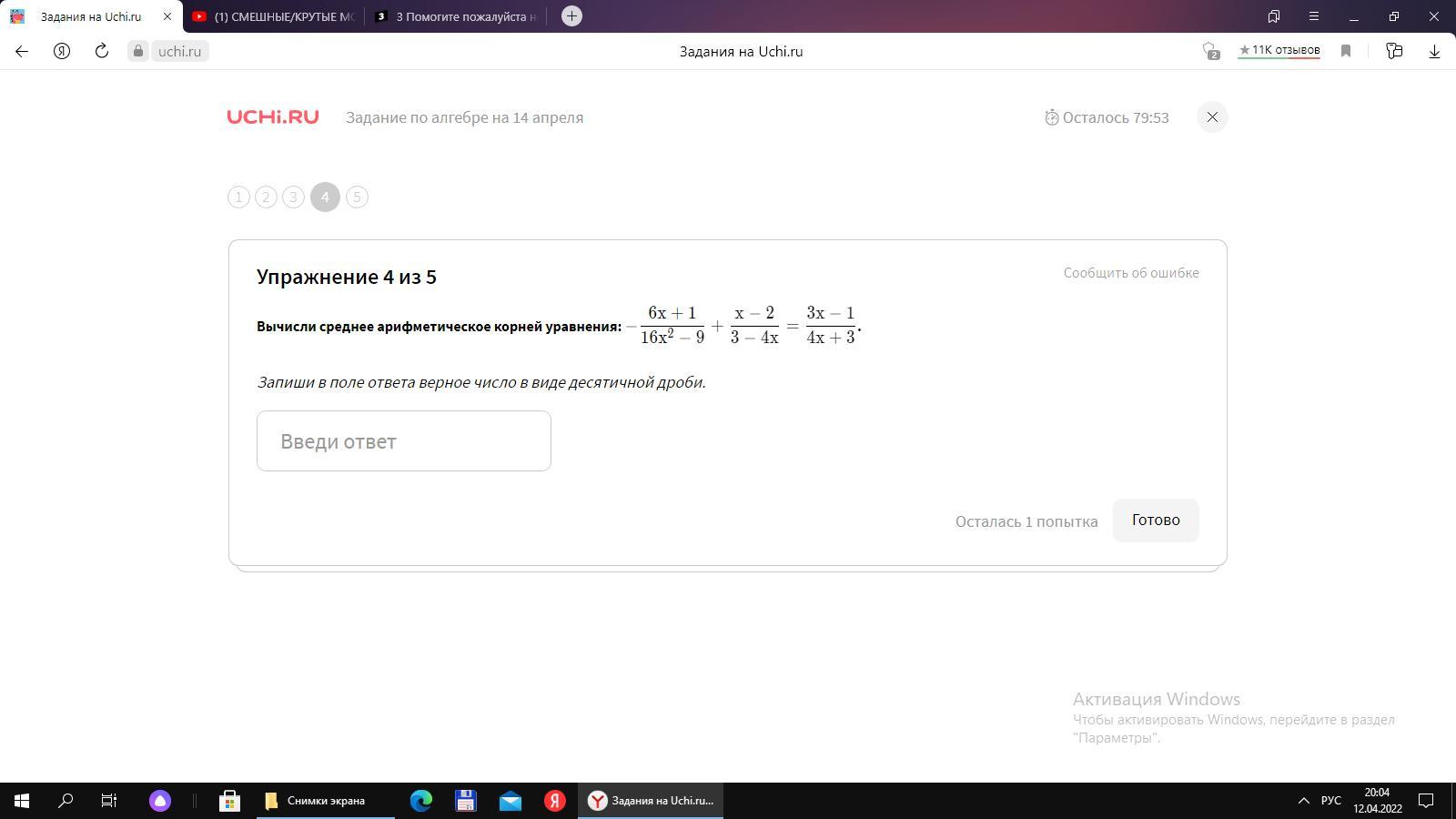
Найдём среднее арифметическое корней уравнения , для этого сложим их и разделим на 2 :
это в виде десятичной дроби?
все правильно спасибо
Не узнали десятичную дробь ?
да
Похожие вопросы
Предмет: Русский язык,
автор: Oksanaf85
Предмет: Другие предметы,
автор: MrCkrelk
Предмет: Русский язык,
автор: нюра25
Предмет: Українська мова,
автор: vitaliyf261
Предмет: Русский язык,
автор: Astra2017