Question

в прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла , равен 6 градусов. Найдите меньший острый угол данного треугольника.(начертить треугольник и решение)​

Answer 1

Ответ:

Меньший острый угол треугольника равен 42°.

Объяснение:

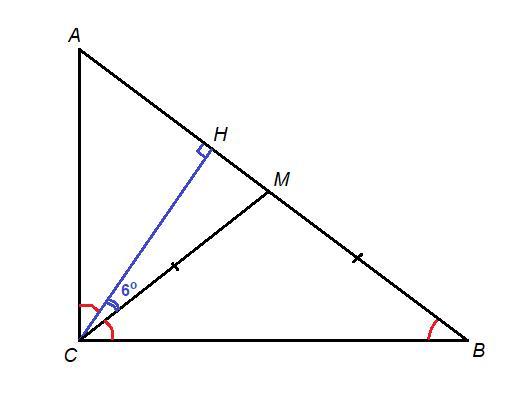
СН - высота, СМ - медиана треугольника АВС.

∠НСМ = 6°

• Медиана, проведенная к гипотенузе, равна ее половине.

СМ = МВ, ΔСМВ равнобедренный, значит

∠МСВ = ∠В

• Сумма острых углов прямоугольного треугольника равна 90°.

Из прямоугольного треугольника АВС:

∠В = 90° - ∠А

Из прямоугольного треугольника АСН:

∠АСН = 90° - ∠А

Из этих двух равенств следует, что

∠АСН = ∠В

∠АСВ = ∠АСН + ∠НСМ + ∠МСВ

90° = ∠В + 6° + ∠В

2 · ∠В = 90° - 6°

2 · ∠В = 84°

∠В = 42°