Как это решить поэтапно...
номер 234
дам 40 баллов

Ответы
Ответ:
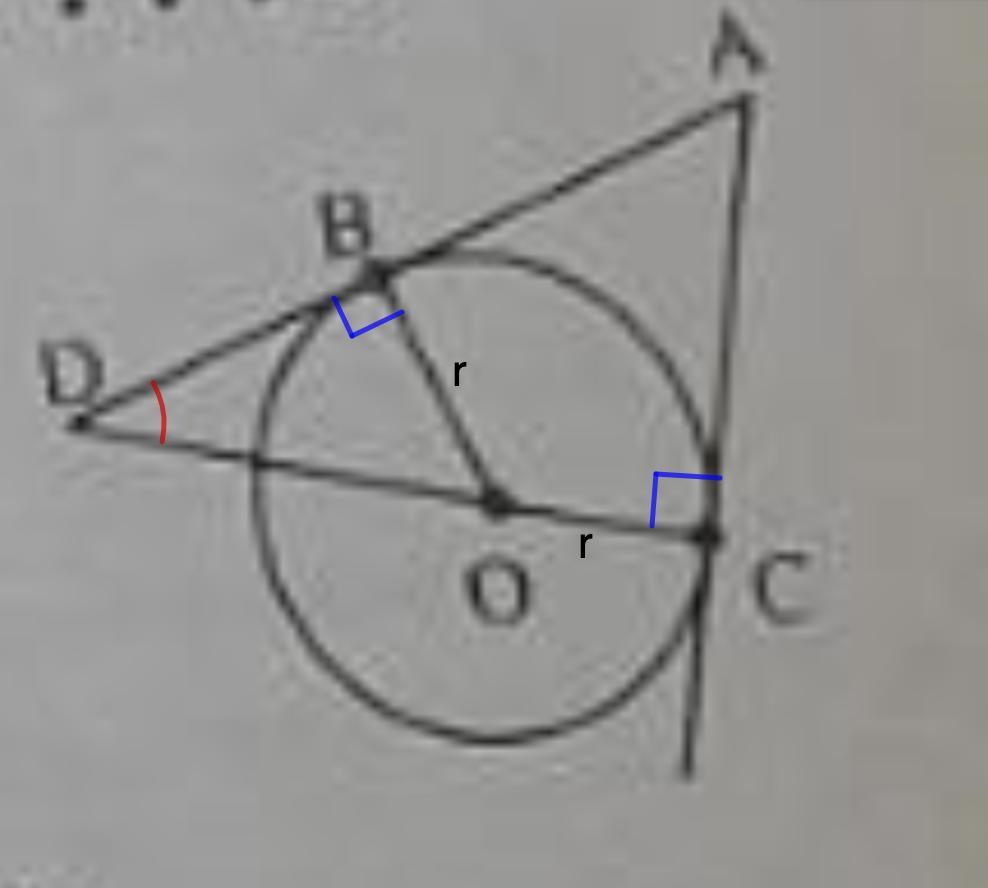
1. Доказано, что ΔADC ~ ΔODB.
2. а) AC = 12 ед.; AD = 20 ед.
б) AC = 7,5 ед.; AD = 19,5 ед.
Объяснение:
Требуется доказать, что ΔADC и ΔODB подобны.
Найти АD и АС, если:
а) OD = 10; OC = 6; б) BD = 12; OD = 13.
Дано: Окр.О;
AD и AC - касательные;
В и С - точки касания.
Доказать: ΔADC ~ ΔODB;
Найти: АD и АС, если
а) OD = 10; OC = 6; б) BD = 12; OD = 13.
Доказательство:
Рассмотрим ΔADC и ΔODB.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ DC ⊥ AC; ОВ ⊥ AD.
ΔADC и ΔODB - прямоугольные.
∠D - общий.
⇒ ΔADC ~ ΔODB (по двум углам).
Решение:
а) ΔADC ~ ΔODB.
OD = 10; OC = 6;
ОВ = OC = 6 (радиусы одной окружности)
Напишем отношения сходственных сторон:
Из ΔODB по теореме Пифагора найдем BD:
BD² = OD² - OB² = 100 - 36 = 64
BD = 8
Найдем АС:
Найдем AD:
AC = 12 ед.; AD = 20 ед.
б) ΔADC ~ ΔODB.
BD = 12; OD = 13.
Из ΔODB по теореме Пифагора найдем BО:
BО² = OD² - DB² = 169 - 144 = 25
BO = 5
BO = OC = 5 (радиусы одной окружности)
Найдем АС:
Найдем AD:
AC = 7,5 ед. ; AD = 19,5 ед.