Question

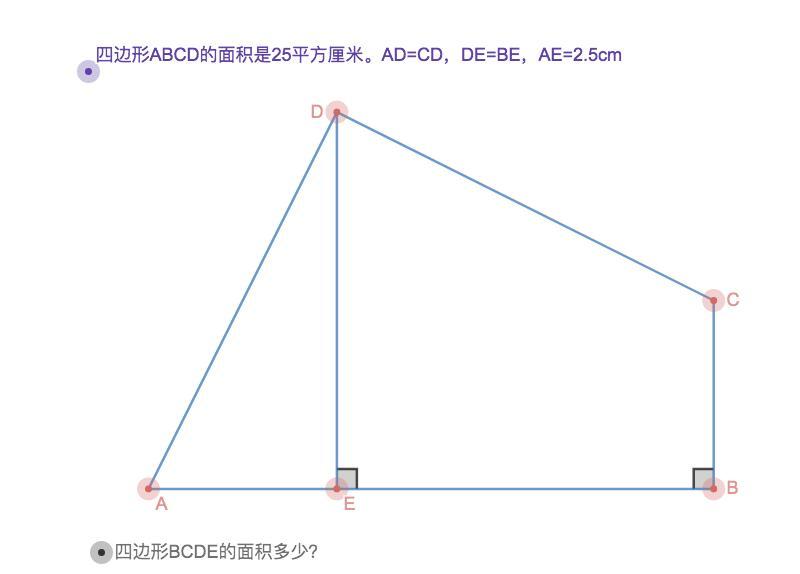
Площадь четырехугольника ABCD составляет 25 квадратных сантиметров.AD=CD,DE=BE,AE=2,5 см

• Какова площадь четырехугольника BCDE?

Answer 1

Ответ:

Sbcde = 18,75 сm.

Объяснение:

Пусть DE = BE = x (дано).

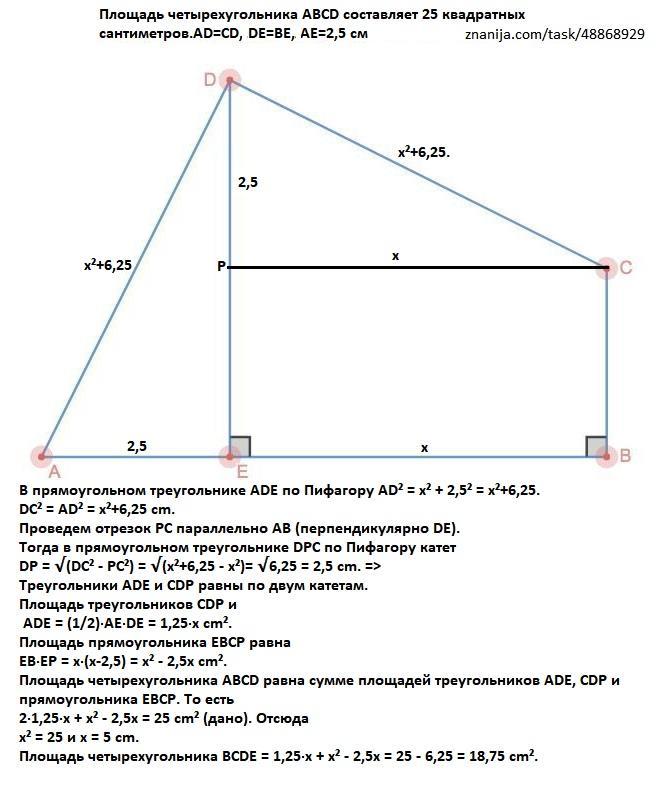
В прямоугольном треугольнике ADE по Пифагору AD² = х² + 2,5² = х²+6,25.

DC² = AD² = х²+6,25 cm.

Проведем отрезок РС параллельно АВ (перпендикулярно DE).

Тогда в прямоугольном треугольнике DPC по Пифагору катет

DP = √(DC² - PC²) = √(х²+6,25 - x²)= √6,25 = 2,5 cm. =>

Треугольники ADE и CDP равны по двум катетам.

Площадь треугольников CDP и

ADE = (1/2)·AE·DE = 1,25·x cm².

Площадь прямоугольника ЕВСР равна

ЕВ·ЕР = х·(х-2,5) = х² - 2,5х cm².

Площадь четырехугольника ABCD равна сумме площадей треугольников ADE, CDP и прямоугольника ЕВСР. То есть

2·1,25·x + х² - 2,5х = 25 cm² (дано). Отсюда

х² = 25 и х = 5 cm.

Площадь четырехугольника BCDE = 1,25·x + х² - 2,5х = 25 - 6,25 = 18,75 cm².