Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить задачу
Приложения:
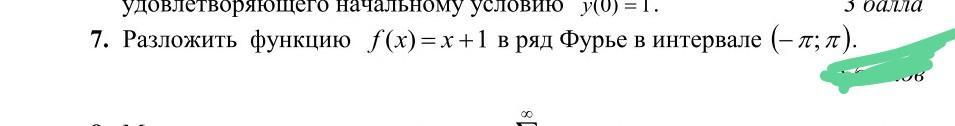
Ответы
Автор ответа:
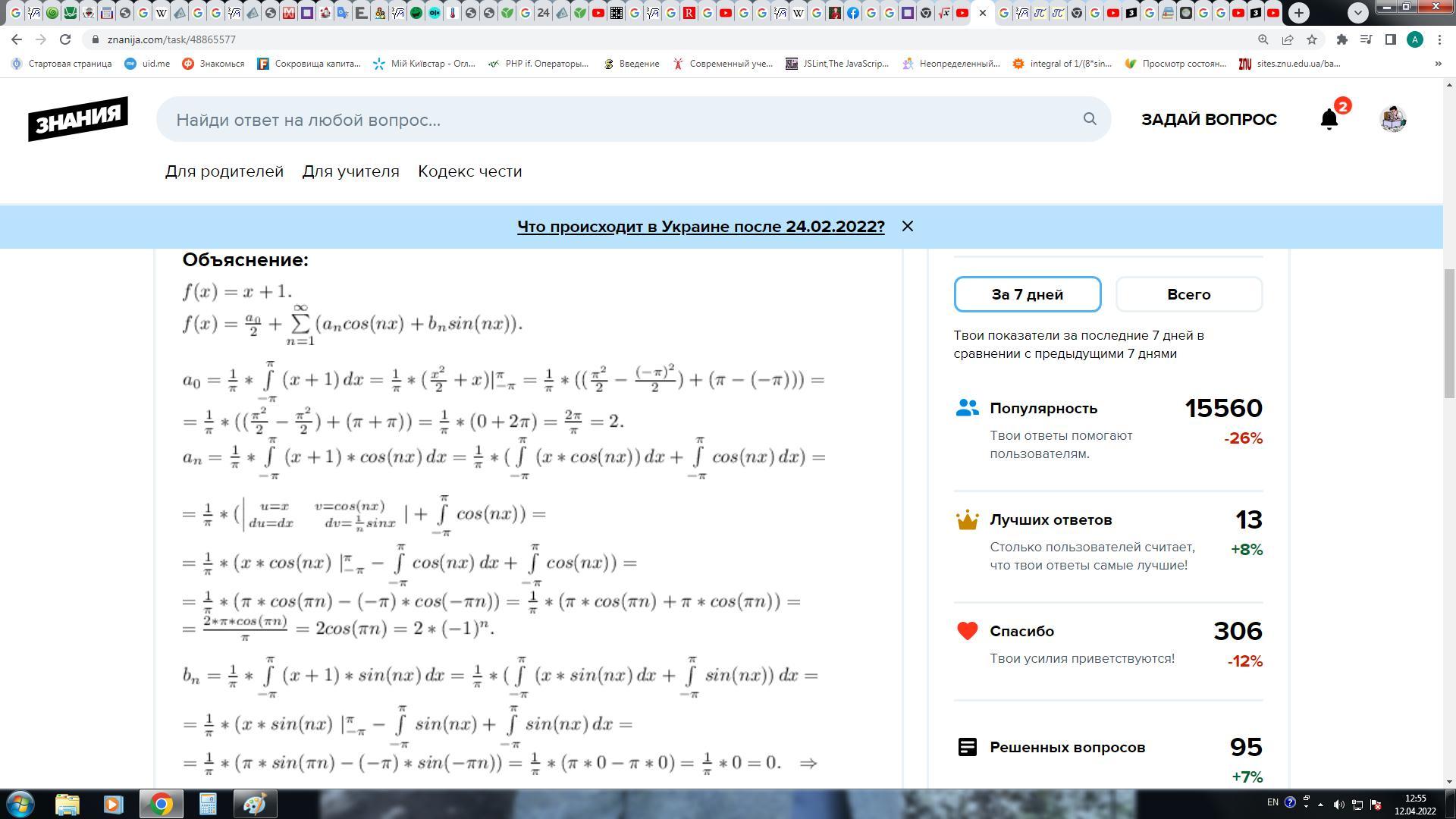
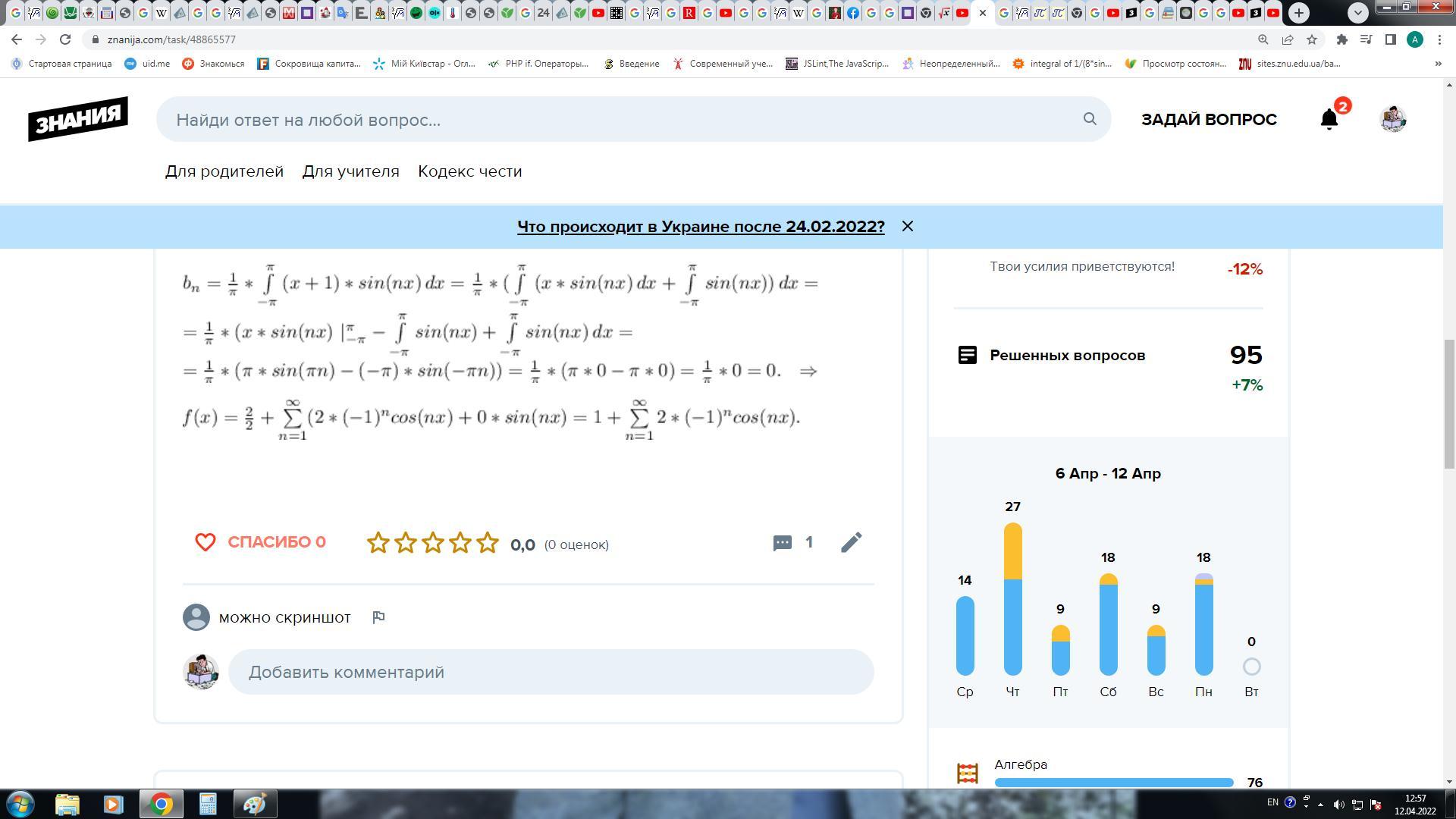
1
Объяснение:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Kasumia
Предмет: Русский язык,
автор: Хас07
Предмет: Русский язык,
автор: Маффи5
Предмет: Биология,
автор: polina213564
Предмет: Русский язык,
автор: tavs79