Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить задачу
Приложения:
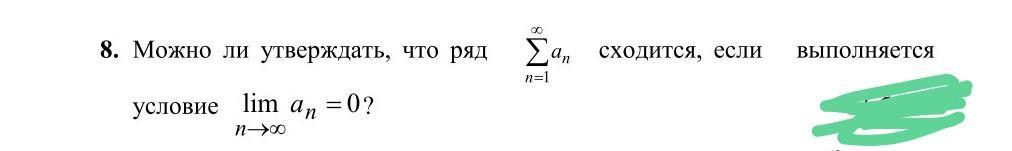
Ответы
Автор ответа:
2
Необходимый признак сходимости ряда.
Если ряд сходится, то его общий член стремится к нулю: .
То есть для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю. Но этого ещё не достаточно . Иными словами, если общий член ряда стремится к нулю, то это ещё не значит, что ряд сходится . Он может как сходится, так и расходится .
Например, у гармонического расходящегося ряда предел общего члена ряда равен нулю,
.
Поэтому проверка условия нужна для определения расходящихся рядов . Если общий член ряда не стремится к нулю
, то ряд расходится .
Ответ: нельзя утверждать, что ряд сходится, если выполня-
ется условие .
Похожие вопросы
Предмет: Технология,
автор: даша718
Предмет: Русский язык,
автор: katrinesina
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: mariy1198