Даю 40 баллов. 8 класс.
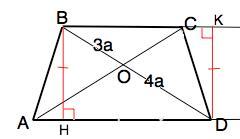
В трапеции ABCD с основаниями AD и BC точка О - точка пересечения диагоналей. BO:OD=3:4. Найдите отношение площадей треугольников ABD и ABC.
Ответы
Ответ: Ѕ(ABD) : Ѕ(ABC)=3:4
Объяснение (подробно):
Сделаем чертёж по условию задачи и проведем высоты: ВН для ∆ АВD и DK для ∆ АВС.
Так как основания трапеции параллельны, а высоты треугольников являются расстоянием между ними, то по свойству параллельных прямых ВН=DK=h - высоте трапеции ABCD.
Треугольники, образованные диагоналями трапеции и их основаниями, подобны по равным накрестлежащим углам при основаниях и вертикальным в точке пересечения диагоналей. =>
ВС:АD=3:4
Площадь треугольника равна половине произведения основания на высоту, проведенную к ней. Высоты треугольников равны.
S(ABC)=h•BC:2
S(ABD)=h•AD:2
Если высоты двух треугольников равны, то отношение их площадей равно отношению их оснований.
S(ABC):S(ABD)=BC:AD=3:4 => Ѕ(ABD) : Ѕ(ABC)=4:3