Предмет: Алгебра,
автор: bulanyanpol
упростите выражение, пожалуйста
Приложения:
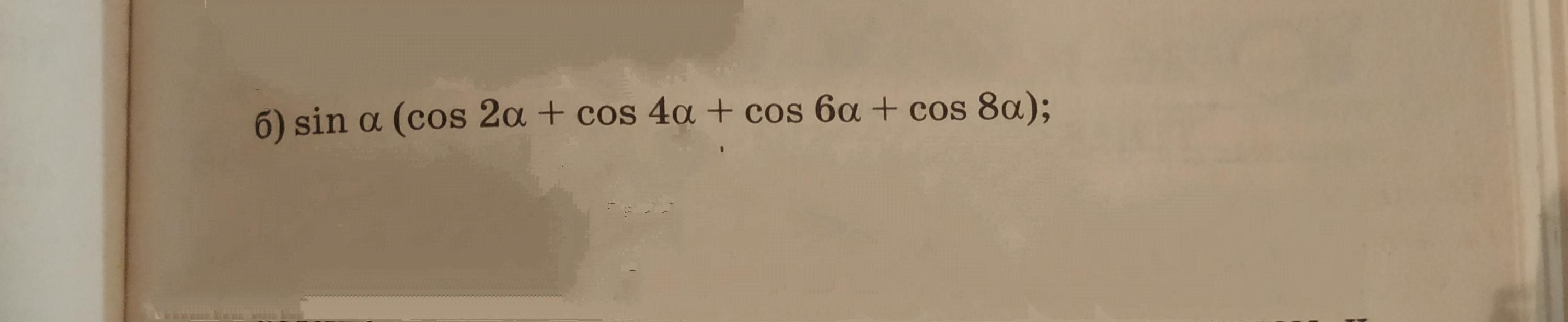
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Окружающий мир,
автор: geforce8230
Предмет: Русский язык,
автор: Nadezhda2006125
Предмет: Қазақ тiлi,
автор: АrmShow
Предмет: Английский язык,
автор: 03081982swetla
Предмет: Русский язык,
автор: Danil200453