Предмет: Алгебра,
автор: Lqdqiaq
Помогите пожалуйста срочно
Приложения:
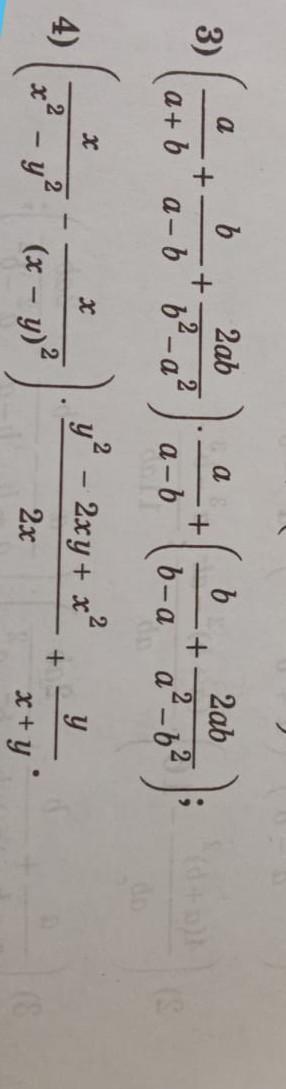
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: EroinaHop
Предмет: Русский язык,
автор: Простоматч222246357
Предмет: Английский язык,
автор: dap
Предмет: Қазақ тiлi,
автор: Asemaa05