Question

помогите пожалуйста (с решением)

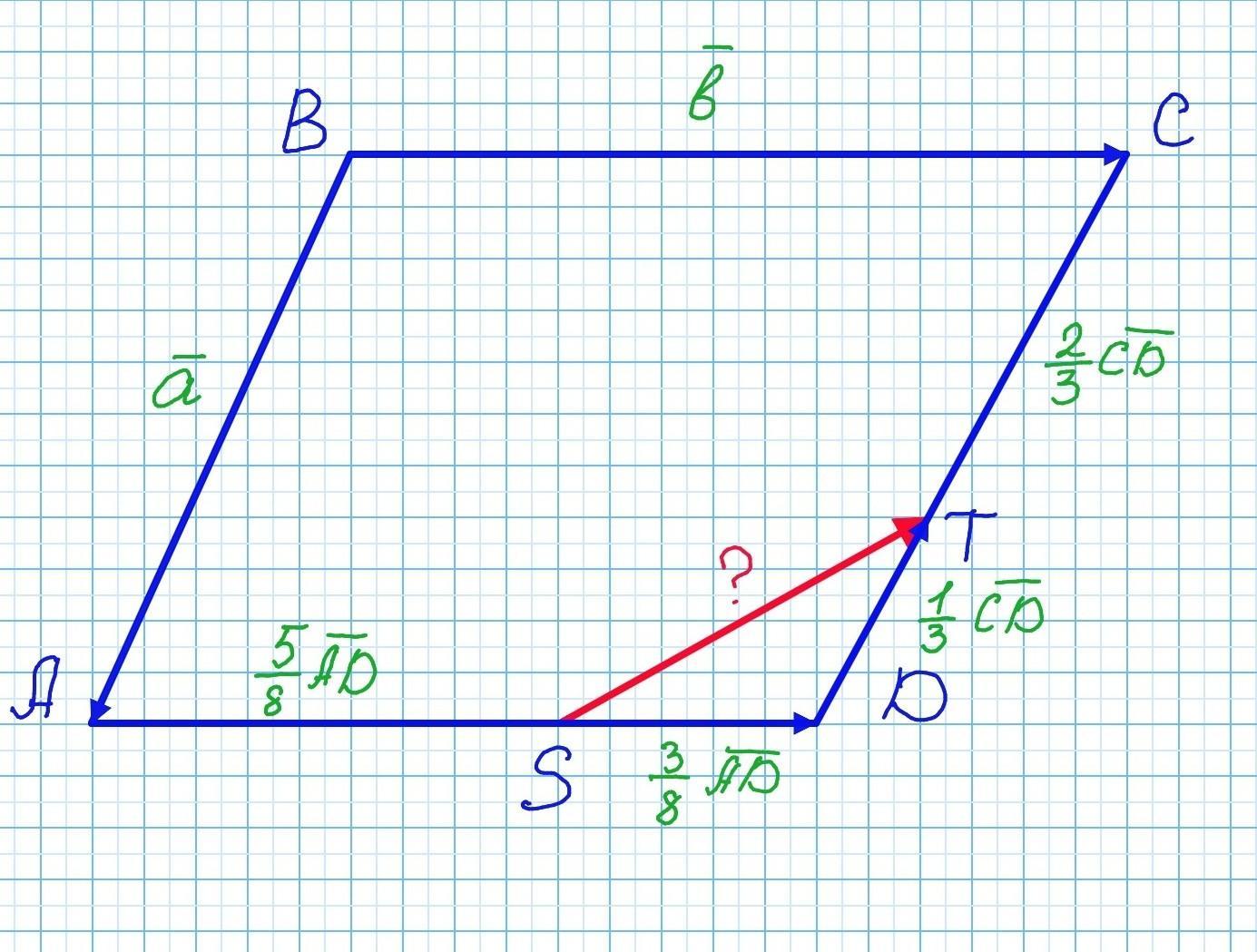
На сторонах AD и CD параллелограмма ABCD отмечены соответственно точки S и T так, что AS: SD = 5:3, СТ: TD = 2:1. Выразите вектор ST через векторы ВА = а и ВС = b​

Answer 1

Ответ:

$\overline{ST} = \dfrac{3}{8} \times \overline{b} - \dfrac{1}{3} \times \overline{a}$

Объяснение:

По правилу треугольника вектор ST равен:

$\overline{ST} = \overline{SD} + \overline{DT}$

Так как у параллелограмма противолежащие стороны равны и параллельны, a вектора $\overline{BA}$ и $\overline{CD}$, а также $\overline{BC}$ и $\overline{AD}$ сонаправленны то:

$\overline{CD} = \overline{BA} = \overline{a} \\ \\ \overline{AD} = \overline{BC} = \overline{b}$

SD составляет 3/8 части от АD (AD равен 8 единиц). Следовательно:

$\overline{SD} = \frac{3}{8} \times \overline{AD} = \frac{3}{8} \times \overline{BC} = \frac{3}{8} \times \overline{b}$

DT составляет 1/3 части от DC (DC равен 3 единицы). Векторы $\overline{DC}$ и $\overline{BA}$ направлены в разные стороны. Поэтому:

$\overline{DT} = \frac{1}{3} \times \overline{DC} = \frac{1}{3} \times ( - \overline{BA}) = - \frac{1}{3} \times \overline{a}$

$\overline{ST} = \frac{3}{8} \times \overline{b} - \frac{1}{3} \times \overline{a}$