Question

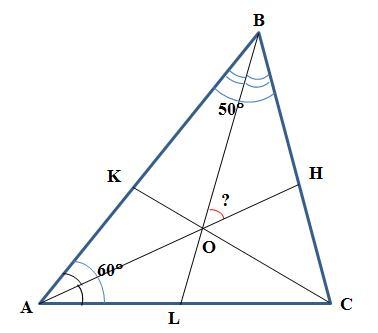
В треугольнике ABC угол A равен 60 градусов, а угол B равен 50 градусов. AH, CK и BL - биссектрисы, проведенные к сторонам треугольника и пересекающиеся в точке O.
Найди угол BOH.

Answer 1

Ответ:

∠BOH = 55°

Пошаговое объяснение:

Дано (см. рисунок):

  ΔABC

  ∠A=60°

  ∠B=50°

  AH, CK и BL - биссектрисы

  O - точка пересечения биссектрис  

Найти: ∠BOH.

Решение. Так как AH биссектриса угла А, то в треугольнике AHB угол HAB = 30°. По теореме о внутренних углах треугольника в треугольнике AHB

∠HAB+∠B+∠AHB=180°.

Отсюда

∠AHB = 180°–∠HAB–∠B = 180°–30°–50° = 100°.

Так как BL биссектриса угла B, то в треугольнике BOH угол OBH = 25°. По теореме о внутренних углах треугольника в треугольнике BOH

∠OHB+∠OBH+∠BOH=180°.

Отсюда

∠BOH=180°–∠OHB–∠OBH.

Но ∠OHB=∠AHB=100° и ∠OBH= 25°. Тогда

∠BOH=180°–100°–25° = 55°.