Question

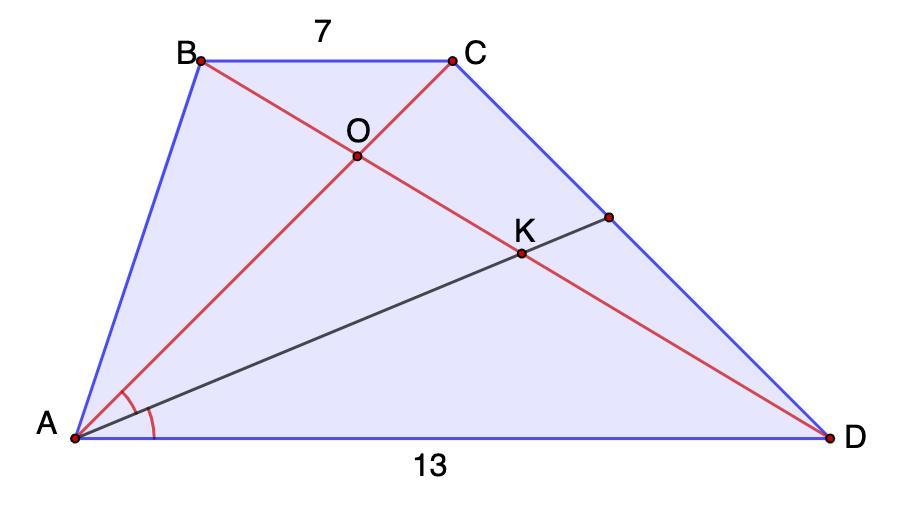
В трапеции ABCD с основаниями AD = 13 и ВС = 7 точка K- середина BD, а луч AK – биссектриса угла CAD. Найдите длину диагонали АС. ​

Answer 1

Ответ:

Длина диагонали АС равна 6 ед.

Объяснение:

В трапеции ABCD с основаниями AD = 13 и ВС = 7 точка K- середина BD, а луч AK – биссектриса угла CAD.

Найдите длину диагонали АС.

Дано: ABCD - трапеция;

AD = 13; ВС = 7;

BK = KD;

AK – биссектриса угла CAD.

Найти: АС.

Решение:

1. Рассмотрим ΔВОС и ΔAOD.

• Вертикальные углы равны.

⇒ ∠ВОС и ∠AOD (вертикальные)

• При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.

⇒ ∠CAD = ∠ACB (накрест лежащие при ВС || AD и секущей АС)

ΔВОС ~ ΔAOD (по двум углам)

Запишем отношения соответственных сторон:

$\displaystyle \boxed { \frac{CO}{OA}=\frac{BO}{OD}=\frac{BC}{AD}=\frac{7}{13} }$     (1)

2. Пусть BО = 7х, тогда OD = 13х

⇒ BD = 7x + 13x = 20x

BK = KD = 20x : 2 = 10x (условие)

⇒ OK = BK - OB = 10х - 7х = 3х

3. Рассмотрим ΔAОD.

AK - биссектриса (условие)

• Биссектриса, проведеная из вершины угла, делит его противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

⇒

$\displaystyle \frac{KO}{OA}=\frac{KD}{AD}\\ \\ \frac{3x}{AO}=\frac{10X}{13}\\ \\ AO = \frac{3x\cdot13}{10x}=\frac{39}{10}$

4. Из равенства (1):

$\displaystyle \frac{CO}{OA} =\frac{7}{13}\\ \\\frac{CO}{\frac{39}{10} }=\frac{7}{13}\\ \\ CO = \frac{39\cdot7}{10\cdot13}=\frac{21}{10}$

5. Найдем АС.

АС = АО + ОС

$\displaystyle AC= \frac{39}{10}+\frac{21}{10}=\frac{60}{10}=6$

Длина диагонали АС равна 6 ед.